Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn:
+ Độ biến dạng của lò xo tại các vị trí cân bằng tạm x 0 = μ m g k = 0 , 05.1.10 100 = 5 m m
Vật bị nén nhiều nhất khi vật chuyển động hết nửa chu kì đầu tiên
→ Trong nửa chu kì đầu vật đi được quãng đường S = 2 X 0 − x 0 = 2 10.10 − 2 − 5.10 − 3 = 0 , 19 m
→ Lực ma sát đã sinh công A = F m s S = μ m g S = 0 , 095 J .
Đáp án C

Đáp án B
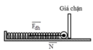
Phương trình động lực học cho vật theo phương ngang: F d h + N = m a , khi vật rời khỏi giá thì N = 0.
→ Δ l = m a k = 1.3 100 = 0 , 03 m
→ Vật sẽ rời giá chặn tại vị trí lò xo bị nén một đoạn 3 cm
+ Thời gian chuyển động của vật từ vị trí ban đầu đến khi rời khỏi giá t = 2 17 3 − 3 .10 − 2 3 = 2 15 s.
Vận tốc của vật khi rời khỏi giá chặn v = a t = 3 2 15 = 40 cm.
→ Biên độ dao động mới A = 3 2 + 40 10 2 = 5 cm.

Chọn C
Tần số góc của dao động ω = k m = 40 0 , 4 = 10 rad/s → T = 0,2π s
+ Tại thời điểm ban đầu vật đang ở vị trí biên, sau khoảng thời gian Δ t = T + T 6 = 7 π 30 s vật đến vị trí có li độ bằng một nửa biên độ → E d = 0 , 75 E E t = 0 , 25 E
+ Giữ điểm chính giữa của lò xo, một nửa thế năng đàn hồi của lò xo sẽ mất đi theo phần chiều dài của lò xo không tham gia dao động → cơ năng của hệ dao động lúc sau sẽ là E ′ = E d + 0 , 5 E t = 0 , 875 E .
+ Với k′ = 2k, ta có 1 2 k ' A ' 2 = 0 , 875 1 2 k A 2 → A ' = A 0 , 875 2 = 8 0 , 875 2 = 2 7 c m

Đáp án C
Phương pháp: Áp dụng hệ thức độc lập với thời gian của li độ và vận tốc
Cách giải:
Ta có:
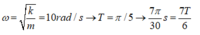
Tại thời điểm ngay trước khi giữ lò xo:
![]()
Sau khi giữ, x giảm một nửa và độ cứng tăng gấp đôi:
![]()

Đáp án C
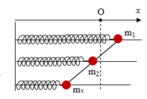
Ta có ω 1 = ω 2 = ω 3 = 10 π rad / s
Phương trình dao động của vật 1 và vật 2 là:
x 1 = 3 cos ( 10 πt - π 2 ) c m x 2 = 1 , 5 cos ( 10 πt ) ( n ế u q u y ư ớ c t ọ a đ ộ x = 1 , 5 = ± A )
Trong quá trình dao động cả ba vật nằm trên một đường thẳng khi 2 x 2 = x 1 + x 3 ⇒ x 3 = 2 x 2 - x 1
tính chất trung bình
Bấm máy tính tổng hợp dao động ta được
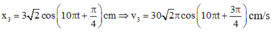
Taị t = 0 và v 30 = - 30 π cm / s
Trường hợp x 2 = 1 , 5 cos ( 10 π t + π ) ( n ế u q u y ư ớ c t ọ a đ ộ x = 1 , 5 = - A )
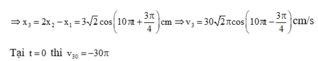

Đáp án A
Biên độ dao động của con lắc A = l m a x − l min 2 = 30 − 22 2 = 4 cm
→ Động năng của con lắc tại vị trí có li độ x
E d = E − E t = 1 2 k A 2 − x 2 = 1 2 .100. 0 , 04 2 − 0 , 03 2 = 0 , 035 J

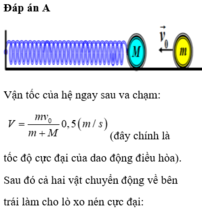
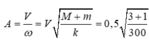

Giả sử mỗi lò xo có độ cứng k --> n lò xo giống nhau ghép song song có độ cứng: n.k
Cơ năng ban đầu của hệ là: \(W=\frac{1}{2}nk.A^2\)
Khi vật tới li độ A/n thì:
+ Thế năng của lò xo: \(W_t=\frac{1}{2}nk.\left(\frac{A}{n}\right)^2\)
+ Động năng \(W_đ\)
Khi tách nhẹ một lò xo ra khỏi hệ thì:
+ Thế năng của lò xo: \(W_{t'}=\frac{1}{2}\left(n-1\right)k.\left(\frac{A}{n}\right)^2\)
+ Động năng \(W_đ\)không đổi.
Như vậy, độ giảm cơ năng của hệ bằng độ giảm thế năng, là: \(\Delta W=W_t-W_{t'}=\frac{1}{2}nk.\left(\frac{A}{n}\right)^2-\frac{1}{2}\left(n-1\right)k.\left(\frac{A}{n}\right)^2=\frac{1}{2}k\left(\frac{A}{n}\right)^2\)
Cơ năng lúc sau: \(W'=W-\Delta W=\frac{1}{2}nkA^2-\frac{1}{2}k\left(\frac{A}{n}\right)^2=\frac{1}{2}\left(n-\frac{1}{n^2}\right)kA^2\)
Mà: \(W'=\frac{1}{2}\left(n-1\right)kA'^2\)
Suy ra: \(\frac{A'}{A}=\sqrt{\frac{n^3-1}{n^2\left(n-1\right)}}=\frac{\sqrt{n^2+n+1}}{n}\)
\(\Leftrightarrow A'=\frac{A}{n}\sqrt{n^2+n+1}\)
Đáp án B.
Cảm ơn nha.