Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn A
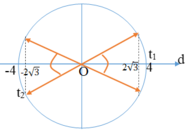
Khoảng cách giữa hai vật theo phương Ox là:
![]()
Theo bài ra ta có d ≥ 2√3
Trong khoảng t1 = 1/24 s đến t2 = 1/3s = t1 + T/2 +T/12, d có độ lớn không nhỏ hơn 2√3 trong khoảng thời gian là:
∆t = T/12 + 2. T/12 = 1/8s.

Ta có: \(a=-\omega^2x\Rightarrow \omega=\sqrt{-\dfrac{a}{x}}=10(rad/s)\)
Ở đây ta phải lấy \(x=-\sqrt 2\) thì mới thoả mãn.
Biên độ: \(A^2=x^2+\dfrac{v^2}{\omega^2}=2+2=4\Rightarrow A = 2(cm)\)
Tìm pha ban đầu: \(\cos\varphi=\dfrac{x_0}{A}=-\dfrac{\sqrt 2}{2}\)
Ban đầy có \(v>0\Rightarrow \varphi<0\)
\(\Rightarrow \varphi =-\dfrac{3\pi}{4}(rad)\)
Vậy: \(x=2\cos(10t -\dfrac{3\pi}{4})(cm)\)

\(A=4\) cm; \(T=\frac{2\pi}{\omega}=2\left(s\right)\)
Góc quét của vecto trên đường tròn:
\(\alpha=2.arcsin\frac{2\sqrt{2}}{4}=2.45^0=90^0\)
\(\Rightarrow\) Vecto quét được \(\frac{1}{4}\) đường tròn \(\Rightarrow t=\frac{T}{4}=\frac{1}{2}\left(s\right)\)