Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

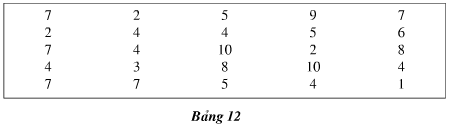
a) Dấu hiệu: tuổi nghề của công nhân trong một phân xưởng. Số các giá trị: 25.
b) Bảng tần số về tuổi nghề
![]()
Nhận xét:
- Số các giá trị của dấu hiệu: 25
- Số các giá trị khác nhau: 10, giá trị lớn nhất là 10, giá trị nhỏ nhất là 1.
- Giá trị có tần số lớn nhất là 4.
-Các giá trị thuộc vào khoảng chủ yếu từ 4 đến 7 năm.

Bảng tần số về tuổi nghề
| Tuổi nghề (năm) | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | |
| Tần số (n) | 1 | 3 | 1 | 6 | 3 | 1 | 5 | 2 | 1 | 2 | N=25 |
Nhận xét:
- Số các giá trị của dấu hiệu: 25
- Số các giá trị khác nhau: 10, giá trị lớn nhất là 10, giá trị nhỏ nhất là 1.
- Giá trị có tần số lớn nhất là 4 (tần số của giá trị 4 là 6).
- Các giá trị chủ yếu là 4 năm hoặc 7 năm.

a)\(\frac{4^2.4^3}{2^{10}}=\frac{4^5}{\left(2^2\right)^5}=\frac{4^5}{4^5}=1\)
b)\(\frac{\left(0,6\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2.5\right)^5}{\left(0,2\right)^6}=\frac{\left(0,2\right)^5.3^5}{\left(0,2\right)^5.0,2}=\frac{3^5}{0,2}=1215\)
c)\(\frac{2^7.9^3}{6^5.8^2}=\frac{2^7.\left(3^2\right)^3}{\left(2.3\right)^5.\left(2^3\right)^2}\)
d) \(\frac{6^3+3.6^2+3^2}{-13}=\frac{2^3.3^3+3^2.2^2+3^3}{-13}=\frac{3^3.\left(2^3.2^2+1\right)}{-13}=-3^3=-27\)

\(a.\sqrt{0,01}-\sqrt{0,25}=\sqrt{0.1^2}-\sqrt{0,5^2}\)
\(=|0.1|-|0,5|=0,1-0,5=-0,4\)
\(\sqrt{0,01}-\sqrt{0,25}\)
\(=\sqrt{\frac{1}{100}}-\sqrt{\frac{25}{100}}\)
\(=\frac{1}{10}-\frac{5}{10}\)
\(=\frac{-2}{5}\)

Dấu hiệu ở đây là tuổi nghề của mỗi công nhân trong một phân xưởng (tính theo năm)
7 có 6 tần số 8 có 5 tần số 5 có 4 tần số a/các giá trị là 7 4 6 8 2 10 5 9
4 có 5 tần số 2 có 2 tần số 9 có 2 tần số
6 có 7 tần số 10 có 1 tần số
CÒN LẠI MÌNH KO BIẾT !!!!$$$



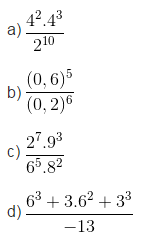
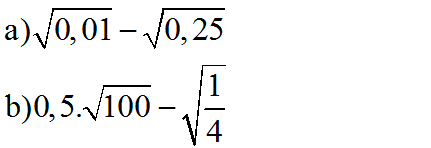
Bạn tham khảo !
a) Dấu hiệu: tuổi nghề của công nhân trong một phân xưởng. Số các giá trị: 25.
b) Bảng tần số về tuổi nghề
Nhận xét:
Số các giá trị của dấu hiệu: 25
Số các giá trị khác nhau: 10, giá trị lớn nhất là 10, giá trị nhỏ nhất là 1.
Giá trị có tần số lớn nhất là 4.
Các giá trị thuộc vào khoảng chủ yếu từ 4 đến 7 năm.