Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) + b) + c)
A B C D H K
Vì chứng minh được câu a) thì khỏi cần chứng minh câu b) và c)
\(S_{ABD}=S_{BDC}\)
- Đáy AB = DC
- Có chiều cao bằng chiều cao của hình bình hành ( AH = BK)
\(S_{ADC}=S_{ABC}\)
- Đáy AB = DC
- Có chiều cao bằng chiều cao hình bình hành
Vì vậy có thể kết luận rằng :\(S_{ABD}=S_{BDC}=S_{ABC}=S_{ACD}\)
\(S_{ABD}=S_{OAB}+S_{AOD}\)
\(S_{ADC}=S_{AOD}+S_{DOC}\)
Vì có chung diện tích AOD nên S OAB = S DOC
Tương tự...

M B C D A H K
Kẻ BH và DK cùng vuông góc với AI.
Ta có \(\widehat{HIB}=\widehat{KAD}\) (so le trong) nên \(\Delta HIB\sim\Delta KAD\left(g-g\right)\)
\(\Rightarrow\frac{BH}{DK}=\frac{BI}{AD}=\frac{BI}{BC}=\frac{1}{2}\)
Lại có: \(S_{ABM}=\frac{1}{2}.m.BH\Rightarrow BH=\frac{2b}{m}\)
Tương tự \(DK=\frac{2d}{m}\)
Suy ra d = 2b hay \(d^2=4b^2.\).
Gọi độ dài cạnh của hình vuông ABCD là a thì BI = a/2.
Xét tam giác vuông ABI, đường cao BH ta có: \(\frac{1}{BH^2}=\frac{1}{AB^2}+\frac{1}{BI^2}\Rightarrow\frac{1}{\left(\frac{2b}{m}\right)^2}=\frac{1}{a^2}+\frac{1}{\left(\frac{a}{2}\right)^2}\)
\(\Leftrightarrow\frac{m^2}{4b^2}=\frac{5}{a^2}\Rightarrow a^2=\frac{4.5b^2}{m^2}=\frac{4}{m^2}\left(4b^2+b^2\right)=\frac{4}{m^2}\left(d^2+b^2\right)\)
Vậy \(S_{ABCD}=\frac{4}{m^2}\left(d^2+b^2\right).\)

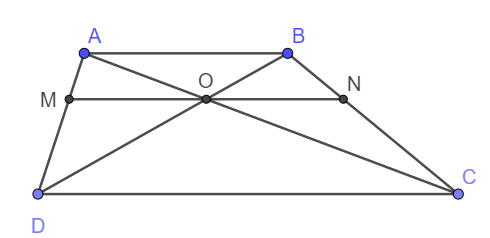
a) Do AB//CD nên áp dụng hệ quả định lý Ta let ta có:
\(\frac{AO}{OC}=\frac{OB}{OD}\) hay \(\frac{DO}{DB}=\frac{OC}{AC}\)
Xét tam giác ABD có OM//AB nên \(\frac{OM}{AB}=\frac{DO}{DB}\)
Tương tự \(\frac{ON}{AB}=\frac{CO}{CA}\)
Vậy nên \(\frac{OM}{AB}=\frac{ON}{AB}\Rightarrow OM=ON\)
b) Coi AB = 1, DC = k thì \(\frac{DO}{OB}=\frac{DC}{AB}=k\Rightarrow\frac{DO}{DB}=\frac{k}{k+1}\)
\(\Rightarrow OM=ON=\frac{k}{k+1}\Rightarrow MN=\frac{2k}{k+1}\)
Ta có \(\frac{1}{AB}+\frac{1}{CD}=\frac{1}{1}+\frac{1}{k}=\frac{k+1}{k}\)
\(\frac{2}{MN}=\frac{2}{\frac{2k}{k+1}}=\frac{k+1}{k}\)
Vậy nên \(\frac{1}{AB}+\frac{1}{CD}=\frac{2}{MN}\)
c) Ta thấy ngay \(\Delta COD\sim\Delta AOB\left(g-g\right)\) theo tỉ lệ k ở câu b.
Vậy thì \(\frac{S_{COD}}{S_{AOB}}=\frac{2009^2}{2008^2}=\left(\frac{2009}{2008}\right)^2=k^2\Rightarrow k=\frac{2009}{2008}\)
Từ đó ta có \(\frac{OC}{OA}=\frac{DO}{OB}=\frac{2009}{2008}\)
Vậy thì \(\frac{S_{ADO}}{S_{AOB}}=\frac{2009}{2008}\Rightarrow S_{ADO}=\frac{2009}{2008}.2008^2=2009.2008\)
\(\frac{S_{BOC}}{S_{AOB}}=\frac{2009}{2008}\Rightarrow S_{BOC}=\frac{2009}{2008}.2008^2=2009.2008\)
Suy ra \(S_{ABCD}=S_{AOB}+S_{DOC}+S_{AOD}+S_{BOC}=2008^2+2009^2+2.2008.2009\)
\(=\left(2008+2009\right)^2=4017^2\left(cm^2\right)\)

tam giác BDE: M là tđ(trung điểm) DE, N là tđ BE => MN là đtb(đường trung bình) của tam giác BDE.=> MN//DB <=> MN//BA
tương tự c/m MQ là đtb của tam giác DEC=> MQ//EC hay MQ//AC. mà AC vuông góc AB=> MN vuông góc PQ.=> góc NMQ =90. tương tự theo cách đtb thì các góc còn lại của tứ giác MNPQ =90=> là hình chữ nhật
MN là đtb=> MN=1/2 DB. MQ=1/2 EC mà EC=DB=> MN=DB
=> tg là hình vuông(dhnb)