Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo
nối đường chéo AC
Trong ∆ABC ta có
E là trung điểm của AB
F là trung điểm của BC
Nên EF là đường trung bình của ∆ABC
EF//=1/2AC(1)
(Sd tính chất của đng trung bình)
Chứng minh tương tự với ∆ADC
=> HG//=1/2AC(2)
Từ (1) và(2) suy ra EF//=HG
Vậy tứ giác EFGHlaf hình bình hành
Vì có một cặp đối song song và bằng nhau

Tự vẽ hình :)
t/g ABC có :
AE = EB
BF = FC
\(\Rightarrow\)EF - đường trung bình của tam giác ABC
\(\Rightarrow\)\(EF\)// \(AC\)\(,\)\(EF=\frac{AC}{2}\left(1\right)\)
t/g ADC có :
AH = HD
CG = GD
\(\Rightarrow\)HG - đường trung bình của tam giác ADC
\(\Rightarrow\)\(HG\)// \(AC\)\(,\)\(HG=\frac{AC}{2}\)\(\left(2\right)\)
Từ ( 1 ) và ( 2 ) \(\Leftrightarrow\)EF // HG , EF = HG
Vì tứ giác EFGH có 2 cạnh đối song song và bằng nhau
\(\Rightarrow\)EFGH - hình bình hành ( đpcm )

Gọi K là trung điểm của AC .
Xét tam giác ADC ta có :
\(AE=DE\)(GT)
\(AK=CK\)(GT)
=> EK là đường trung bình của tam giác ADC
\(\Rightarrow EK=\frac{1}{2}CD\)
Xét tam giác ABC ta có :
\(BF=CF\)(GT)
\(KA=KC\)(GT)
=> KF là đường trung bình của tam giác ABC
+) Xét tam giác EFK ta có :
\(EF\le EK+KF\)
Mà \(EK=\frac{1}{2}CD\)( chứng minh trên )
\(KF=\frac{1}{2}AB\)( chứng minh trên )
\(\Rightarrow EK+KF=\frac{CD}{2}+\frac{AB}{2}\)
\(=\frac{AB+CD}{2}\)
Vậy \(EF\le\frac{AB+CD}{2}\) ( đpcm)

Áp dụng tính chất đường trung bình của tam giác ta chứng minh được:
E H = F G = 1 2 B D v à H G = E F = 1 2 A C
Mà AC = BD Þ EH = HG = GF= FE nên EFGH là hình thoi.
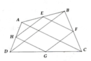

a: Xét ΔABC có
E là trung điểm của BC
F là trung điểm của CA
Do đó: EFlà đường trung bình
=>EF//AB và EF=AB/2(1)
Xét ΔABD có
H là trung điểm của DB
G la trung điểm của AD
Do đó: HG là đường trung bình
=>HG//AB và HG=AB/2(2)
Từ (1) và (2) suy ra HG//FE và HG=FE
b: HE=DC/2
EF=AB/2
mà AB=DC
nên HE=FE
Xét tứ giác EFGH có
EF//GH
EF=GH
Do đó: EFGH là hình bình hành
mà EH=EF
nên EFGH là hình thoi

Sửa đề; EG=FH
Xét ΔABD có
E,H lần lượt là trung điểm của AB,AD
=>EH là đường trung bình
=>EH//BD và EH=BD/2(1)
Xét ΔCBD có
F,G lần lượt là trung điểm của CG,CD
=>FG là đường trung bình
=>FG//BD và FG=BD/2(2)
Từ (1), (2) suy ra EH//FG và EH=FG
Xét tứ giác EHGF có
EH//FG
EH=FG
=>EHGF là hình bình hành
mà EG=FH
nên EHGF là hình chữ nhật
=>EH vuông góc HG
mà EH//BD
nên BD vuông góc HG
mà HG//AC
nên AC vuông góc BD

a) x4+x3+2x2+x+1=(x4+x3+x2)+(x2+x+1)=x2(x2+x+1)+(x2+x+1)=(x2+x+1)(x2+1)
b)a3+b3+c3-3abc=a3+3ab(a+b)+b3+c3 -(3ab(a+b)+3abc)=(a+b)3+c3-3ab(a+b+c)
=(a+b+c)((a+b)2-(a+b)c+c2)-3ab(a+b+c)=(a+b+c)(a2+2ab+b2-ac-ab+c2-3ab)=(a+b+c)(a2+b2+c2-ab-ac-bc)
c)Đặt x-y=a;y-z=b;z-x=c
a+b+c=x-y-z+z-x=o
đưa về như bài b
d)nhóm 2 hạng tử đầu lại và 2hangj tử sau lại để 2 hạng tử sau ở trong ngoặc sau đó áp dụng hằng đẳng thức dề tính sau đó dặt nhân tử chung
e)x2(y-z)+y2(z-x)+z2(x-y)=x2(y-z)-y2((y-z)+(x-y))+z2(x-y)
=x2(y-z)-y2(y-z)-y2(x-y)+z2(x-y)=(y-z)(x2-y2)-(x-y)(y2-z2)=(y-z)(x2-2y2+xy+xz+yz)