Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a. hạ đương cao AK
suy ra BK=KC=3:2=1.5(cm)
Xét tam giac ABC có góc AKB=90
AK^2+BK^2=AB^2(đl py-ta-go)
AK=\(\dfrac{3\sqrt{3}}{2}\)
SABC=\(\dfrac{1}{2}.\dfrac{3\sqrt{3}}{2}.3=\dfrac{9\sqrt{3}}{4}\)

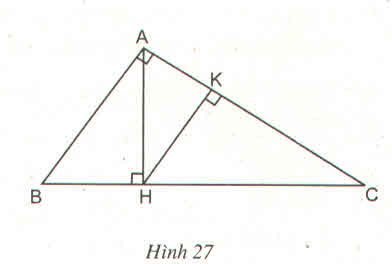
, Tự vẽ hình và ghi giả thiết kết luận (mình không biết vẽ hình trên máy -_-")
Giải : Từ giả thiết ta có
D là trung điểm của AB và MO
,E là trung điểm của AC và ON
=> ED là đường trung bình của cả hai tam giác ABC và OMN
Áp dụng định lý đường trung bình vào tam giác trên ,ta được
\(\hept{\begin{cases}AD//BC,DE//MN\\DE=\frac{1}{2}BC,DE=\frac{1}{2}MN\end{cases}}\Rightarrow\hept{\begin{cases}MN//BC\\MN=BC\end{cases}}\)
Tứ giác MNCB có hai cạnh đối song song và bằng nhau nên nó là hình bình hành
Từ từ ,hình như mình làm nhầm đề :) Để mình làm lại đã rồi trả lời bn sau nhé!!!!!@@

chờ tí :)
bẹn tự vẽ hình nhé
Ta có 2 phân giác của hai góc kề bù thì vuông góc với nhau => \(MB\perp BN\)hay \(\widehat{MBN}=1v\);
\(AM\perp BM,AN\perp BN\left(gt\right)\Rightarrow\widehat{AMB}=\widehat{ANB}=1v\)
Như vậy, tứ giác AMBN có 3 góc vuông là hình chữ nhật.
CM tương tự ta có : tứ giác APCQ là hcn
Biết rằng trong 1 hcn hai đường chèo = nhau và cắt nhau tại trung điểm mỗi đường=> đường chéo MN đi qua trung điểm E của AB.
Mặt khác: EB=EN => tam giác EBN cân tại E => góc ABN = ANB
Mà ABN = NBC (gt) => ABN=ANB
tức là MN//BC ( THEO dấu hiệu nhận biết hai đường thẳng song2)
Như vậy MN vừa đi qua trung điểm E của AB lại vừa // với BC nên M,N phải nằm trên đường trung bình EF của tam giác ABC.
Lập luận tương tự ta sẽ có P,Q cũng nằm trên đường trung bình EF của tam giác ABC -> nên chúng thẳng hàng(đpcm)