Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a: Xét ΔOBC có OB=OC
nên ΔOBC cân tại O
mà \(\widehat{CBO}=60^0\)
nên ΔOBC đều
Xét ΔOCM có
CB là đường trung tuyến
CB=OM/2
Do đó: ΔOCM vuông tại C
hay MC là tiếp tuyến của (O)

a, Vì OCB là tam giác đều nên BC=BO=BM=R
=> O C M ^ = 90 0 => MC là tiếp tuyến (O;R)
b, Ta có: O M 2 = O C 2 + M C 2
=> M C 2 = 3 R 2

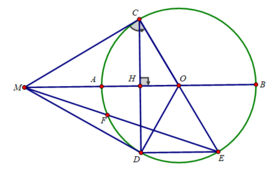
a) Xét tam giác COD cân tại O có OH là đường cao
⇒ OH cũng là tia phân giác ⇒ ∠(COM) = ∠(MOD)
Xét ΔMCO và ΔMOD có:
CO = OD
∠(COM) = ∠(MOD)
MO là cạnh chung
⇒ ΔMCO = ΔMOD (c.g.c)
⇒ ∠(MCO) = ∠(MDO)
∠(MCO) = 90 0 nên ∠(MDO) = 90 0
⇒ MD là tiếp tuyến của (O)

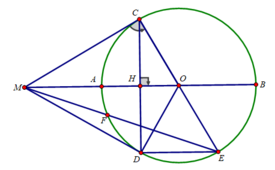
d) Ta có: ∠(CFE) = 90 0 (F thuộc đường tròn đường kính CE)
Lại có CF là đường cao nên MC 2 = MF.ME
Tương tự, ta có: MC 2 = MH.MO
⇒ ME.MF = MH.MO
⇒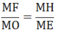
Xét ΔMOF và ΔMEN có:
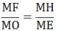
∠(FMO) chung
⇒ ΔMOF ∼ ΔMEN (c.g.c)
⇒ ∠(MOF) = ∠(MEH)
Bài 1:
a: Ta có: ΔOBC cân tại O
mà OH là đường cao
nên OH là phân giác của góc BOC
Xét ΔOBA và ΔOCA có
OB=OC
\(\widehat{BOA}=\widehat{COA}\)
OA chung
Do đó: ΔOBA=ΔOCA
=>\(\widehat{OBA}=\widehat{OCA}\)
=>\(\widehat{OCA}=90^0\)
=>AC là tiếp tuyến của (O)
b: Xét (O) có
ΔBKD nội tiếp
BD là đường kính
Do đó: ΔBKD vuông tại K
=>BK\(\perp\)KD tại K
=>BK\(\perp\)AD tại K
Xét ΔABD vuông tại B có BK là đường cao
nên \(AK\cdot AD=AB^2\left(1\right)\)
Xét ΔABO vuông tại B có BH là đường cao
nên \(AH\cdot AO=AB^2\left(2\right)\)
Từ (1) và (2) suy ra \(AK\cdot AD=AH\cdot AO\)
Câu 8:
a: Xét (O) có
ΔCAB nội tiếp
AB là đường kính
Do đó: ΔCAB vuông tại C
=>\(\widehat{CAB}+\widehat{CBA}=90^0\)
=>\(\widehat{CBA}=60^0\)
Xét ΔOBC có OB=OC và \(\widehat{OBC}=60^0\)
nên ΔOCB đều
=>BC=OB=R
=>BO=BM=R
=>B là trung điểm của OM
Xét ΔOCM có
CB là đường trung tuyến
CB=1/2OM
Do đó: ΔOCM vuông tại C
b: Ta có: OB+BM=OM
=>OM=R+R=2R
Ta có: ΔOCM vuông tại C
=>\(OC^2+CM^2=OM^2\)
=>\(CM^2=\left(2R\right)^2-R^2=3R^2\)