Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

gọi số cần tìm là abcdef (a#0 ; a;b;c;d;e;f € A ; f chẵn )
f có 3 cách chọn
a có 5 cách chọn lọc
b;c;d;e đều có 6 cách chọn
=> có 3*5*6*6*6*6 = 19440 số thỏa mãn yêu cầu bài toán
b) gọi số cần tìm là abcdef (a#0;f=0,5 ; a;b;c;d;e;f € A )
f=0,5 => f có 2 cách chọn
a có 5 cách chọn
b;c;d;e đều có 6 cách chọn
=> có 2*5*6*6*6*6 = 12960

1. số tự nhiên có dạng abce ( nhớ gạch trê đầu ( vì đây là số tự nhiên))
* ta có h là :
h= mn
trong đó tập hợp mn là {0,1}
=> có 2 trường hợp xảy ra
(m,n)=(1,0) hoặc (0,1)
* ta có số tự nhiên abhe có tập hợp {h,2,3,4,5,6,7,8,9}
a có 9 cách chọn
b có 8 cách chọn
c có 7 cách chọn
e có 6 cách chọn
vậy có 9*8*7*6=3024 số
*ta phải loại trường hợp h đứng đầu và có dạng 01
trường hợp h đứng đầu và có dạng 01 có số cách chọn là :
a có 1 cách chọn là h
b có 8 cách
c có 7 cách
e có 6 cách
=> có 1*8*7*6=336 số
vậy số tự nhiên theo yêu cầu đề bài có tổng cộng
3024 - 332688 số
0 chắc

Số tự nhiên thỏa mãn có dạng với a,b,c,d ∈ A và đôi một khác nhau.
TH1: d=0
Có 5 cách chọn a; 4 cách chọn b và 3 cách chọn c nên theo quy tắc nhân có 5.4.3 = 60 số.
TH2: d ≠ 0 ; d có 2 cách chọn là 2, 4
Khi đó có 4 cách chọn a( vì a khác 0 và khác d); có 4 cách chọn b và 3 cách chọn c.
Theo quy tắc nhân có: 2.4.4.3=96 số
Vậy có tất cả: 96 + 60 = 156 số.

Số tam giác là \(C_{2n}^3\). Một đa giác đều 2n đỉnh thì có n đường chéo xuyên tâm. Cứ 2 đường chéo xuyên tâm thì có một hình chữ nhật theo yêu cầu. Vậy số hình chữ nhật là \(C_n^2\).
Theo bài ta có phương trình :
\(C_{2n}^3=20C_n^2,\left(n\ge2\right)\)
\(\Leftrightarrow\frac{\left(2n\right)!}{\left(2n-3\right)!3!}=20\frac{n!}{\left(n-2\right)!2!}\)
\(\Leftrightarrow\frac{\left(2n-2\right)\left(2n-1\right)2n}{3}=20\left(n-1\right)n\)
\(\Leftrightarrow2\left(n-1\right)\left(2n-1\right)2n=60\left(n-1\right)n\)
\(\Leftrightarrow2n-1=15\), (do \(n\ge2\))
\(\Leftrightarrow n=18\)
Vậy đa giác đều có 16 cạnh, (thập lục giác đều)

Ta có 5 cách chọn hàng chục và bốn cách chọn hàng đơn vị nên ta có 4*5=20 số

a) () // (ABCD) =>
// AB =>
là trung điểm của SB. Chứng minh tương tự với các điểm còn lại
b) Áp dụng định lí Ta-lét trong không gian:
\(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}\).
Do \(A_1A_2=A_2A\) nên : \(\dfrac{A_1A_2}{A_2A}=\dfrac{B_1B_2}{B_2B}=\dfrac{C_1C_2}{CC_2}=\dfrac{D_1D_2}{D_2D}=1\).
Nên \(B_1B_2=B_2B;C_1C_2=CC_2=D_1D_2=D_2D\).
c) Có hai hình chóp cụt:



Xếp số vào 9 ô trống thỏa yêu cầu đề bài:
Bước 1: Chọn 2 ô trong 8 ô (bỏ ô đầu tiên) để xếp hai chữ số 0, có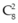 cách chọn.
cách chọn.
Bước 2: Chọn 3 ô trong 7 ô còn lại để xếp ba chữ số 2, có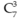 cách.
cách.
Bước 3: Chọn 2 ô trống trong 4 ô còn lại để xếp 2 chữ số 3, có cách chọn.
cách chọn.
Bước 4: Hai ô còn lại xếp 2 chữ số còn lại, có 2! Cách xếp.
Theo quy tắc nhân có: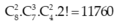
số thỏa yêu cầu bài toán.
Chọn B.