
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.



Đặt A = -x2 - y2 + xy + 2x + 2y
=> 4A = -4x2 - 4y2 + 4xy + 8x + 8y
= -(4x2 - 4xy + y2) + 4(2x - y) - 4 - 3y2 + 12y - 12 + 16
= -(2x - y)2 + 4(2x - y) - 4 - 3(y2 - 4y + 4) + 16
= -(2x - y - 2)2 - 3(y - 2)2 + 4 \(\le16\)
=> A \(\le4\)
=> Max A = 4
Dấu "=" xảy ra <=> \(\hept{\begin{cases}2x-y-2=0\\y-2=0\end{cases}}\Leftrightarrow\hept{\begin{cases}x=2\\y=2\end{cases}}\)
Vậy Max A = 4 <=> x = y = 2


Bài 3:
a) Ta có: \(\left(x+10\right)^2+\left(x-10\right)^2\)
\(=x^2+20x+100+x^2-20x+100\)
\(=2x^2+200\)
b) Ta có: \(\left(x-12\right)^2+\left(x+12\right)^2\)
\(=x^2-24x+144+x^2+24x+144\)
\(=2x^2+288\)
c) Ta có: \(\left(x+7\right)^2-\left(x-7\right)^2\)
\(=\left(x+7-x+7\right)\left(x+7+x-7\right)\)
\(=14\cdot2x\)
=28x
Bài 1:
a) Ta có: \(\left(a+12\right)^2\)
\(=a^2+2\cdot a\cdot12+12^2\)
\(=a^2+24a+144\)
b) Ta có: \(\left(3a+\dfrac{1}{3}\right)^2\)
\(=\left(3a\right)^2+2\cdot3a\cdot\dfrac{1}{3}+\left(\dfrac{1}{3}\right)^2\)
\(=9a^2+2a+\dfrac{1}{9}\)
c) Ta có: \(\left(5a^2+6\right)^2\)
\(=\left(5a^2\right)^2+2\cdot5a^2\cdot6+6^2\)
\(=25a^4+60a^2+36\)
d) Ta có: \(\left(\dfrac{1}{2}+4b\right)^2\)
\(=\left(\dfrac{1}{2}\right)^2+2\cdot\dfrac{1}{2}\cdot4b+\left(4b\right)^2\)
\(=\dfrac{1}{4}+4b+16b^2\)
e) Ta có: \(\left(a^m+b^n\right)^2\)
\(=\left(a^m\right)^2+2\cdot a^m\cdot b^n+\left(b^n\right)^2\)
\(=a^{2m}+2a^mb^n+b^{2n}\)

a) ĐKXĐ \(\left\{{}\begin{matrix}a^2-4\ne0\\a+2\ne0\\2-a\ne0\\a-2+\dfrac{10-a^2}{a+2}\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a\ne2\\a\ne-2\\\dfrac{a^2-4+10-a^2}{a+2}\ne0\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}a\ne2\\a\ne-2\end{matrix}\right.\)
Ta có:
\( A=\left(\dfrac{a}{a^2-4}+\dfrac{1}{a+2}+\dfrac{2}{2-a}\right):\left[\left(a-2\right)+\dfrac{10-a^2}{a+2}\right]\\ =\dfrac{a+\left(a-2\right)-2\left(a+2\right)}{\left(a-2\right)\left(a+2\right)}:\dfrac{a^2-4+10-a^2}{a+2}\\ =\dfrac{-6}{\left(a-2\right)\left(a+2\right)}\cdot\dfrac{a+2}{6}=\dfrac{-1}{a-2}\)
b) Để
\(A=-\dfrac{1}{a-2}=2007^0=1\\ \Rightarrow a-2=-1\Leftrightarrow a=1\left(t.m\right)\)
c) Để A<0
\(\Leftrightarrow\dfrac{-1}{a-2}< 0\Leftrightarrow a-2>0\Leftrightarrow a>2\left(t.m\right)\)


\(5x\left(3x^2y-2xy^2+1\right)-3xy\left(5x^2-3xy\right)+x^2y^2-10=0\)
\(\Leftrightarrow15x^3y-10x^2y^2+5x-15x^3y+9x^2y^2+x^2y^2-10=0\)
\(\Leftrightarrow5x-10=0\Leftrightarrow x-2=0\Leftrightarrow x=2\)

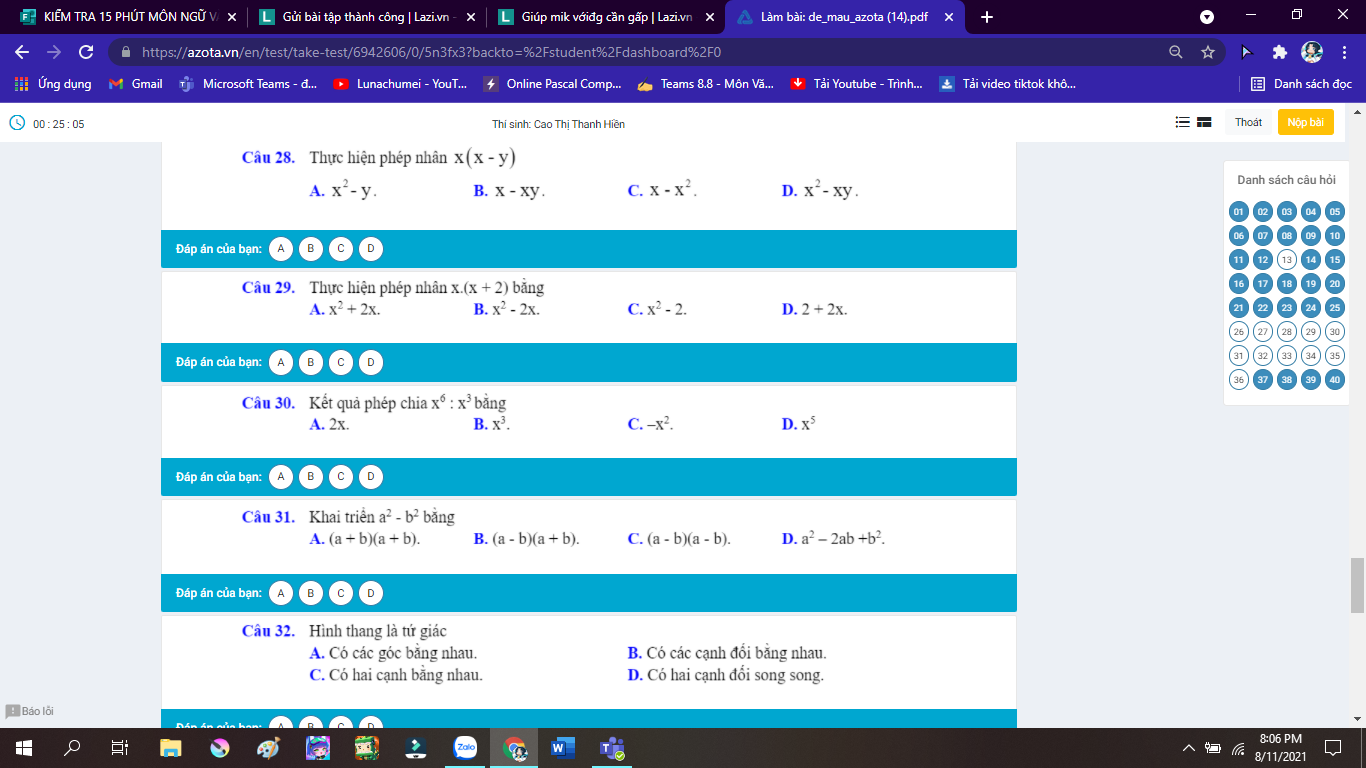
Câu 1:C
Câu 2: A
Câu 3: A
Câu 4: C
Câu 5: C
Câu 6: D
Câu 7: D
Câu 8: A
Câu 10: C

\(3,\)
Vì đa thức có nghiệm là \(\dfrac{1}{2}\) nên \(P\left(\dfrac{1}{2}\right)=\dfrac{1}{4}a+\dfrac{5}{2}-3=0\)
\(\Leftrightarrow\dfrac{1}{4}a=\dfrac{1}{2}\Leftrightarrow a=2\)
\(4,\)
\(a,P\left(x\right)=3-2x=0\Leftrightarrow x=\dfrac{3}{2}\)
\(b,Q\left(x\right)=x^2+2\ge2>0\)
Vậy \(Q\left(x\right)\) luôn dương hay \(Q\left(x\right)\) vô nghiệm

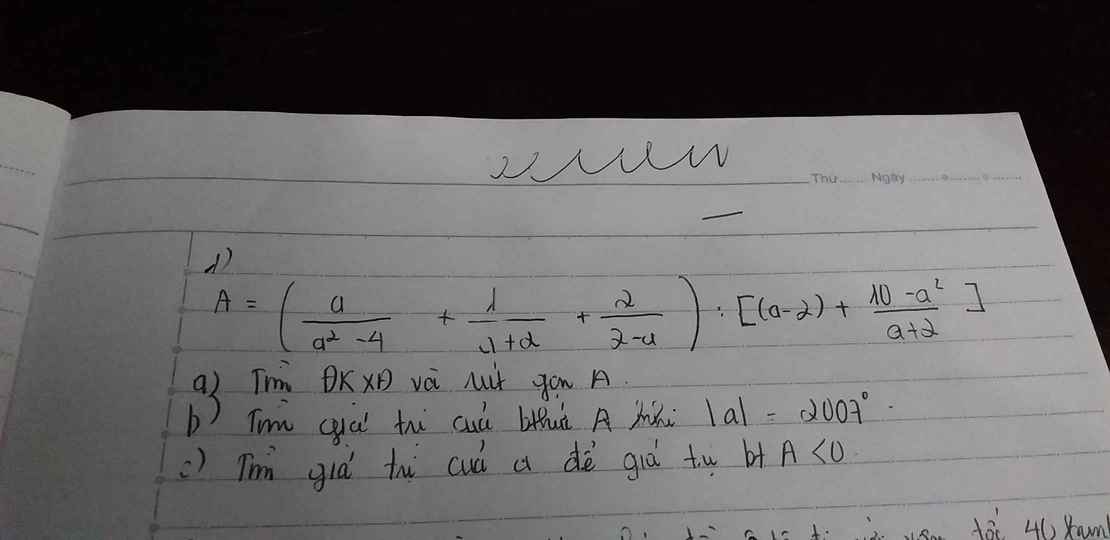

 giúp mình vs mik đg cần gấp
giúp mình vs mik đg cần gấp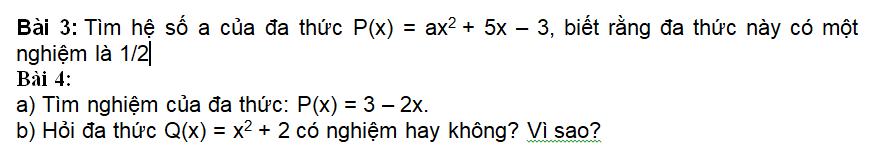
a, 7 - x = -2x + 3
<=> 7 - x + 2x - 3 = 0
<=> x + 4 = 0
<=> x = -4
Vậy....
b, 2(3x+1) = -2x+5
<=> 6x + 2 + 2x - 5 = 0
<=> 8x - 3 = 0
<=> 8x = 3
<=> x = 3/8
Vậy....
c, 5x + 2(x-1) = 4x + 7
<=> 5x + 2x - 2 - 4x - 7 = 0
<=> 3x - 9 = 0
<=> 3x = 9
<=> x = 3
Vậy....
d, 10x2 - 5x(2x + 3 ) = 15
<=> 10x2 - 10x2 - 15x = 15
<=> -15x = 15
<=> x = -1
Vậy....
e, \(\frac{2}{5}x-\frac{1}{10}=x+2\)
\(\Leftrightarrow\)\(\frac{2}{5}x-\frac{1}{10}-x-2=0\)
\(\Leftrightarrow\)\(\frac{-3}{5}x-\frac{21}{10}=0\)
\(\Leftrightarrow\)\(\frac{-3}{5}x=\frac{21}{10}\)
\(\Leftrightarrow\)\(x=\frac{-7}{2}\)
Vậy....
f, \(\frac{1}{2}\left(2x+3\right)+\frac{1}{3}x=\frac{1}{12}\)
\(\Leftrightarrow\)\(x+\frac{3}{2}+\frac{1}{3}x-\frac{1}{12}=0\)
\(\Leftrightarrow\)\(\frac{4}{3}x+\frac{17}{12}=0\)
\(\Leftrightarrow\)\(\frac{4}{3}x=\frac{-17}{12}\)
\(\Leftrightarrow\)\(x=\frac{-17}{16}\)
Vậy.....