Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

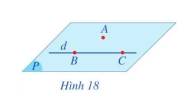
Mặt phẳng (ABC) chứa điểm A và đường thẳng d.
Do đó mp(ABC) cũng chứa hai đường thẳng AB và BC.

1:
a: \(D\in SA\subset\left(SAB\right);E\in SB\subset\left(SAB\right)\)
Do đó: \(DE\subset\left(SAB\right)\)
b: \(F\in AB\subset\left(SAB\right)\)
\(F\in DE\subset\left(CDE\right)\)
Do đó: \(F\in\left(SAB\right)\cap\left(CDE\right)\)
2:
\(N\in AB\subset\left(ABM\right);N\in CD\subset\left(SCD\right)\)
Do đó: \(N\in\left(ABM\right)\cap\left(SCD\right)\)
\(M\in SC\subset\left(SCD\right);M\in MB\subset\left(ABM\right)\)
Do đó: \(M\in\left(ABM\right)\cap\left(SCD\right)\)
Do đó: \(\left(ABM\right)\cap\left(SCD\right)=MN\)

Tham khảo:
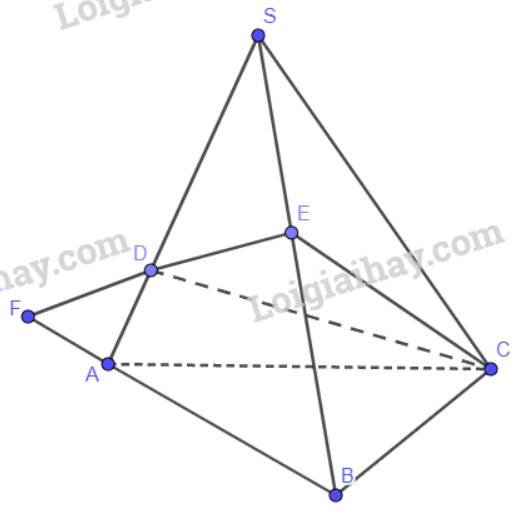
a) Ta có các điểm D, E đều nằm trong mp(SAB) nên đường thẳng DE nằm trong mp (SAB).
b) F thuộc AB suy ra F nằm trong mp (SAB).
F thuộc DE suy ra F nằm trong mp(CDE).
Do đó, F là điểm chung của hai mặt phẳng (SAB) và (CDE).

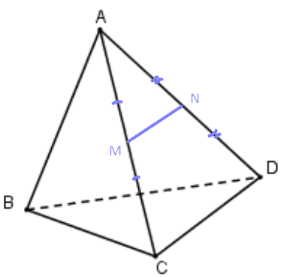
a) Ta có AM cắt (BCD) tại C suy ra AM không song song với (BCD).
b) M, N là trung điểm của AC, AD nên MN là đường trung bình của tam giác ACD suy ra MN // CD.
Mà CD thuộc (BCD) nên MN // mp(BCD).

a) Mặt phẳng đi qua ba điểm A, B, C đi qua đường thẳng d
b) Có một và chỉ một mặt phẳng đi qua điểm A và đường thẳng d

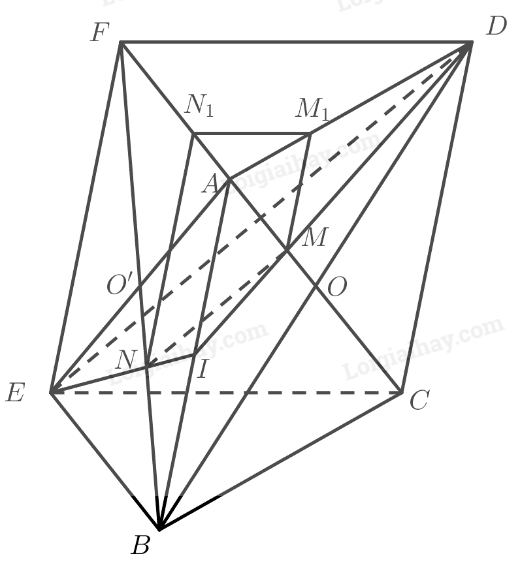
\(\begin{array}{l}\left. \begin{array}{l}N{N_1}\parallel AB \Rightarrow \frac{{A{N_1}}}{{AF}} = \frac{{BN}}{{BF}} = \frac{1}{3}\\M{M_1}\parallel AB \Rightarrow \frac{{A{M_1}}}{{A{\rm{D}}}} = \frac{{IM}}{{I{\rm{D}}}} = \frac{1}{3}\end{array} \right\} \Rightarrow \frac{{A{N_1}}}{{AF}} = \frac{{A{M_1}}}{{A{\rm{D}}}}\\\left. \begin{array}{l} \Rightarrow {M_1}{N_1}\parallel DF\\DF \subset \left( {DEF} \right)\end{array} \right\} \Rightarrow {M_1}{N_1}\parallel \left( {DEF} \right)\end{array}\)
c) Ta có:
\(\left. \begin{array}{l}\left. \begin{array}{l}N{N_1}\parallel AB\parallel EF\\EF \subset \left( {DEF} \right)\end{array} \right\} \Rightarrow N{N_1}\parallel \left( {DEF} \right)\\{M_1}{N_1}\parallel \left( {DEF} \right)\\{M_1}{N_1},N{N_1} \subset \left( {MN{N_1}{M_1}} \right)\end{array} \right\} \Rightarrow \left( {MN{N_1}{M_1}} \right)\parallel \left( {DEF} \right)\)

M ∈ BC mà BC ∈ (ABC) nên M ∈ (ABC)
Vì A ∈ (ABC) và M ∈ (ABC) nên mọi điểm thuộc AM đều thuộc (ABC) hay AM ⊂ (ABC)

\(BC\) \(\subset\)\(\left(SBC\right)\)
Tìm giao tuyến của của \(\left(OMN\right)\)và \(\left(SBC\right)\):
\(N\)là điểm chung thứ nhất
Ta có : \(MO\)\(\subset\)\(\left(AMO\right)\)\(\equiv\)\(\left(SAH\right)\)với \(H=AO\)\(\cap\) \(BC\)
\(\left(SAH\right)\)\(\cap\) \(\left(SBC\right)\)= \(SH\)
Trong \(\left(SAH\right)\): \(MO\)\(\cap\) \(SH\)= \(K\)
\(K\)là điểm chung thứ 2.
Vậy \(\left(OMN\right)\)\(\cap\)\(\left(SBC\right)\)= \(NK\)
Trong \(\left(SBC\right):\)\(NK\)\(\cap\)\(BC\)= \(P\)
Vậy \(\left(OMN\right)\)\(\cap\) \(BC\)= \(P\)
Ta có N thuộc (OMN)
C thuộc đường thẳng BC
Mà N trùng với C => N là giao điểm của (OMN) và BC
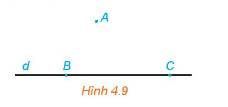
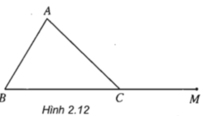
Đưởng thẳng MN có hai điểm phân biệt M, N thuộc mặt phẳng (ABC) nên đường thẳng MN nằm trong mặt phẳng (ABC).