Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cách giải: Đáp án C.
+ Gọi Δx là độ dịch chuyển của vân sáng, Δy là độ dịch chuyển của nguồn sáng .
Vân tối sáng bậc 2 thành vân tối bậc 2 => Δx = 5i
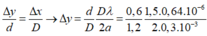
= 0,64 mm

- Gọi Δx là độ dịch chuyển của vân sáng, Δ y là độ dịch chuyển của nguồn sáng.
→ Vân tối sáng bậc 2 thành vân tối bậc 2 → Δ x = 0,5i.
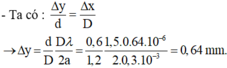

\(i = \frac{\lambda D}{a} =\frac{0,5. 1}{0,5}=1mm.\)
Số vân sáng trên trường giao thoa L là
\(N_s = 2.[\frac{L}{2i}]+1= 2.2.6+1 = 13.\)
Số vân tối trên trường giao thoa L là
\(N_t = 2.[\frac{L}{2i}+0,5]= 2.7 = 14.\)

Khoảng vân : \(i=\frac{0,5.2}{1}=1(mm) \)
Vân tối : x = ki ( k bán nguyên – vân tối bậc 4 → k = 3,5→ x = 3,5mm

+ Ban đầu M là vân tối thứ 3 nên: \(x_M=\left(2+\frac{1}{2}\right)\frac{\lambda D}{a}\left(1\right)\)
+ Khi giãm S1S2 một lượng \(\Delta\)a thì M là vân sáng bậc n nên: \(x_M=n\frac{\lambda D}{a-\Delta a}\left(2\right)\)
+ Khi tăng S1S2 một lượng \(\Delta\)a thì M là vân sáng bậc 3n nên: \(x_M=3n\frac{\lambda D}{a+\Delta a}\left(3\right)\)
+ (2) và (3) \(\Rightarrow k\frac{\lambda D}{a-\Delta a}=3k\frac{\lambda d}{a+\Delta a}\Rightarrow\Delta a=\frac{a}{2}\)
+ Khi tăng S1S2 một lượng 2\(\Delta\)a thì M là sáng bậc k nên: \(x_M=k\frac{\lambda D}{a+2\Delta a}=2,5\frac{\lambda D}{a}\left(4\right)\)
+ Từ (1) và (4) \(\Rightarrow\) k = 5. Vậy tại M lúc này là vân sáng bậc 5.

\(i_1 = \frac{\lambda_1 D}{a}\\ i_2 = \frac{\lambda_2 D}{a}\)=> \( \frac{i_1}{i_2}= \frac{\lambda _1}{\lambda_2}= \frac{540}{600}=0,9.\)
=> \(i_2 = \frac{i_1}{0,9}=0,4 mm.\)

Xây dựng từ phần lý thuyết, hiệu đường đi của ánh sáng từ hai khe đến vân tối thứ \(k+1\) là
\(d_2-d_1 = (k+0,5)\lambda.\)
Áp dụng với \(k+1 = 3\) => \(d_2-d_1 = (2+0,5)\lambda = 2,5 \lambda.\)


Đáp án C.
+ Gọi ∆ x là độ dịch chuyển của vân sáng, ∆ y là độ dịch chuyển của nguồn sáng .
Vân tối sáng bậc 2 thành vân tối bậc 2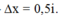
+ Ta có