Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Đáp án A
+ Lần thứ nhất: Ánh sáng dùng trong thí nghiệm có hai loại bức xạ λ1 = 0,5µm và λ2
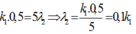
- Trong khoảng giữa hai vân sáng cùng màu với vạch sáng trung tâm có 4 vạch màu của λ2 => vị trí vân trùng của 2 bức xạ ứng với vị trí vân sáng bậc 5 của λ2 :
- Mà 
+ Lần thứ 2: Ánh sáng dùng trong thí nghiệm có ba loại bức xạ λ1 = 0,5µm
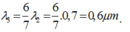
- Vị trí vân sáng trùng nhau của 3 bức xạ thoả mãn:
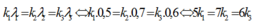
- BCNN(5;6;7)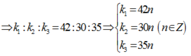 
- Trong khoảng giữa 2 vạch sáng gần nhau nhất và cùng màu với vạch sáng trung tâm (n = 0; n = 1) có tổng 41 vân sáng của λ1; 29 vân sáng của λ1; 34 vân sáng của λ3
=> Tổng số vân sáng của 3 bức xạ là: N = 41 + 29 + 34 = 104 vân. (*)
- Số vân sáng trùng nhau của hai bức xạ λ1 và λ2:
Ta có: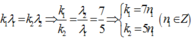 
Trong khoảng giữa 2 vạch sáng gần nhau nhất và cùng màu với vạch sáng trung tâm (n = 0; n = 1) có 5 vân trùng nhau của hai bức xạ λ1 và λ2 (ứng với n1 = 1; 2; 3; 4; 5). (**)
- Số vân sáng trùng nhau của hai bức xạ λ1 và λ3:
Ta có: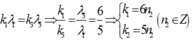 
Trong khoảng giữa 2 vạch sáng gần nhau nhất và cùng màu với vạch sáng trung tâm (n = 0; n = 1) có 6 vân trùng nhau của hai bức xạ λ1 và λ3 (ứng với n2 = 1; 2; 3; 4; 5; 6). (***)
- Số vân sáng trùng nhau của hai bức xạ λ2 và λ3:
Ta có: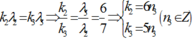 
Trong khoảng giữa 2 vạch sáng gần nhau nhất và cùng màu với vạch sáng trung tâm (n = 0; n = 1) có 4 vân trùng nhau của hai bức xạ λ2 và λ3 (ứng với n3 = 1; 2; 3; 4). (****)
Từ (*),(**),(***),(****) => số vạch sáng đơn sắc quan sát được: Ns = N – 2(5 + 6 + 4) = 104 – 30 = 74.
Ta có công thức xác định vị trí vân trung tâm:
$k_1.\lambda_1=k_2.\lambda_2 =k_3.\lambda_3$
Ta có trong khoảng giữa 2 vân sáng liên tiếp cùng màu với vân trung tâm có 11 vân đỏ thì có 12 khỏang vân ứng với vân đỏ, hay là $k_3 =12$.
Từ đó ta có $k_1=20; k_2 =15$.
Vậy có 14 vân lục và 19 vân tím.
Chọn đáp án C.
\(i=\frac{\lambda D}{a}\Rightarrow\)để vân sáng có màu giống màu vân trung tâm thì
\(i_1=i_2=i_3\Rightarrow k_1\lambda_1=k_2\lambda_2=k_3\lambda_3\)
\(\Rightarrow k_1:k_2:k_3=\frac{1}{0,4}:\frac{1}{0,5}:\frac{1}{0,6}=15:12:10\)
\(\Rightarrow\)khoảng cách giữa các vân sáng có màu giống vân trung tâm là:
\(i=k_1\frac{\lambda_1D}{a}=k_2\frac{\lambda_2D}{a}=k_3\frac{\lambda_3D}{a}=12mm\)
Vậy trong khoảng \(\text{MN=6cm=60mm }\) có
\(\frac{60}{12}=5\)vân sáng (tính cả M và N) cùng màu vân trung tâm.
Đáp án A
Phương pháp: Công thức tính số vân sáng trên bề rộng miền giao thoa L:
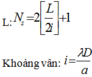
Cách giải:
+ Khoảng vân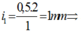 
Số vân sáng của bức xạ λ1 là:
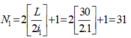
Khoảng vân 
Số vân sáng của bức xạ λ2 là:
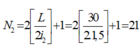
Vị trí vân sáng của hai bức xạ λ1 và λ2 trùng nhau thoả mãn:
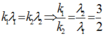
=> Khoảng vân trùng:
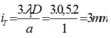
=> Số vân sáng trùng nhau của hai bức xạ là:
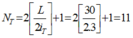
Vậy số vạch màu quan sát được trên vùng giao thoa: N = N1 + N2 – NT = 31+21 – 11 = 41 vạch
Tại vân trung tâm là vân sáng của bước sóng 1 trùng vân sáng của bước sóng 2. Vậy các vân sáng có màu giống vân trung tâm là nơi trùng nhau của vân sáng của bước sóng 1 và vân sáng của bước sóng 2. Vậy ta đi tìm số vị trí trùng nhau.
Ta có: $\frac{{{\lambda _1}}}{{{\lambda _2}}} = \frac{{{k_2}}}{{{k_1}}} = \frac{3}{2}$
$\Rightarrow {k_1} = 2n$
Các vị trí vân sáng của bước sóng 1 và 2 trùng nhau có tọa độ $x = {k_1}\frac{{{\lambda _1}D}}{a}$ (dùng ${k_2}$ cũng được)
Vì $x \le \frac{L}{2}\Leftrightarrow {k_1}\frac{{{\lambda _1}D}}{a} \le \frac{L}{2}$
$\Leftrightarrow 2n\frac{{{\lambda _1}D}}{a} \le \frac{L}{2}$ (với $n$ là số nguyên dương)
$\Leftrightarrow n = 2$
=>có $2n+1=5$ vị trí trùng nhau.
Đáp số : 5
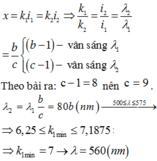
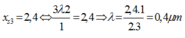
Đáp án D
Phương pháp: Vị trí vân trùng nhau: x1 = x2 <=> k1λ1 = k2λ2
Cách giải:
Vị trí trùng nhau của ánh sáng đỏ và lam:
Trong khoảng giữa hai vân sáng có màu cùng màu với vân sáng trung tâm có 6 vân màu lam => kl chạy từ 0 đến 9
Ta có bảng sau:
kl
0
1
2
3
4
5
6
7
8
9
kd
0
1
2
3
4
5
6
=> Có 3 vân sáng màu đỏ (ứng với k = 1; 3; 5)