Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

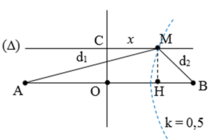
Hai nguồn A và B dao động ngược pha thì tại điểm bất kì trên đường thẳng nối A với B, cách A một khoảng d1 và cách B một khoảng d2 sẽ có vân có biên độ dao động cực tiểu khi
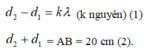
Với k = 0 thì d2 = d1 = 10 cm → vân chính giữa qua O là một vân có biên độ dao động cực tiểu.
M gần O nhất có biên độ cực tiểu thì M thuộc vân cực tiểu thứ nhất, ta lấy
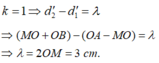

Þ có 13 vân cực tiểu, mỗi vân cắt đường elip tại hai điểm,suy ra số điểm dao động với biên độ cực tiểu trên đường elip là 26.
Đáp án C

Đáp án A
+ Tần số góc của khung dây ω = 2 πn = 2 π . 50 = 100 π rad / s rad/s
→ Suất điện động cảm ứng cực đại
E 0 = ωNBS = 100 π . 500 . 2 5 π . 220 . 10 - 4 = 220 2 V .

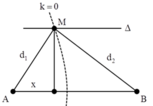
+ Để M là cực tiểu và gần trung trực của của AB nhất thì M phải nằm trên cực tiểu ứng với k = 0.
→ d2 – d1 = (0 + 0,5)λ = 1 cm.
Từ hình vẽ, ta có:
d 1 2 = 2 2 + x 2 d 2 2 = 2 2 + 8 − x 2 → 2 2 + 8 − x 2 − 2 2 + x 2 = 1
→ Giải phương trình trên ta thu được x = 3,44 cm.
Vậy khoảng cách ngắn nhất giữa M và trung trực AB là 4 – 3,44 = 0,56 cm.
Đáp án A

Đáp án A.
Lời giải chi tiết:
Giả sử hai nguồn có phương trình dao động ![]()
Gọi d là khoảng cách từ M tới 2 nguồn, phương trình sóng tại M là:
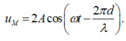
Phương trình sóng tại O là: 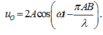
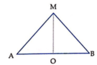
Độ lệch pha giữa chúng 
Để M và O cùng pha thì:
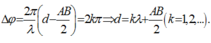
Vì M gần O nhất ứng với k=1
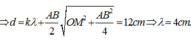
Tốc độ truyền sóng ![]()

Đáp án D
+ Số dãy cực đại trên đoạn
![]()
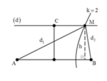
+ Để CM là lớn nhất thì M thuộc hypebol ứng với k=2
Ta có d 1 - d 2 = 8 cm
+ Với:
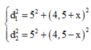
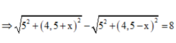
![]()

+ Tại M dao động cực đại nên d 2 − d 1 = k M λ = 4 , 5
+ Vì giữa M và đường trung trực AB còn có 2 cực đại nữa nên k M = 3 ® λ = 1 , 5 cm
+ Tại C là cực đại nên d 2 − L = k C λ = 1 , 5 k C (1)
+ Vì tam giác ABC vuông tại A nên ta lại có: d 2 2 − L 2 = 8 2 (2)
+ Từ (1) và (2) ® L = 64 − 2 , 56 k C 2 3 , 2. k C
+ Để Lmax thì k C = 1 ® L = 19 , 2 ≈ 20 , 6 cm.
ü Đáp án B





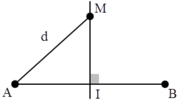

Do hai nguồn AB dao động cùng pha, nên trung điểm O của AB dao động cực đại.
Điểm M cách O một khoảng gần nhất không dao động \(\Rightarrow MO = \dfrac{\lambda}{4}=0,5cm\)
\(\Rightarrow \lambda = 2cm\)
Số điểm dao động cực đại trên AB là: \([\dfrac{9,4}{2}].2+1=9\)
bạn ơi sao lại là \(\dfrac{\text{λ }}{4}\) ?/