Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

\(i = \frac{\lambda D}{a} =\frac{0,5. 1}{0,5}=1mm.\)
Số vân sáng trên trường giao thoa L là
\(N_s = 2.[\frac{L}{2i}]+1= 2.2.6+1 = 13.\)
Số vân tối trên trường giao thoa L là
\(N_t = 2.[\frac{L}{2i}+0,5]= 2.7 = 14.\)

Khoảng vân : \(i=\frac{0,5.2}{1}=1(mm) \)
Vân tối : x = ki ( k bán nguyên – vân tối bậc 4 → k = 3,5→ x = 3,5mm

+ Ban đầu M là vân tối thứ 3 nên: \(x_M=\left(2+\frac{1}{2}\right)\frac{\lambda D}{a}\left(1\right)\)
+ Khi giãm S1S2 một lượng \(\Delta\)a thì M là vân sáng bậc n nên: \(x_M=n\frac{\lambda D}{a-\Delta a}\left(2\right)\)
+ Khi tăng S1S2 một lượng \(\Delta\)a thì M là vân sáng bậc 3n nên: \(x_M=3n\frac{\lambda D}{a+\Delta a}\left(3\right)\)
+ (2) và (3) \(\Rightarrow k\frac{\lambda D}{a-\Delta a}=3k\frac{\lambda d}{a+\Delta a}\Rightarrow\Delta a=\frac{a}{2}\)
+ Khi tăng S1S2 một lượng 2\(\Delta\)a thì M là sáng bậc k nên: \(x_M=k\frac{\lambda D}{a+2\Delta a}=2,5\frac{\lambda D}{a}\left(4\right)\)
+ Từ (1) và (4) \(\Rightarrow\) k = 5. Vậy tại M lúc này là vân sáng bậc 5.

Khi đặt thêm một bản thủy tinh mỏng trước nguồn S1 thì hệ vân sẽ dịch chuyển về phía S1 một đoạn là
\(x = \frac{e(n-1)D}{a}= \frac{12.0,5.1}{1}=6 mm.\)

Khi đặt màn và ảnh cố định, dịch chuyển thấu kính sẽ có 2 vị trí cho ảnh rõ nét
Trường hợp đầu vật cách thấu kính d1 ảnh cách thấu kính d1'
Do tính chất thuận nghịch của ánh sáng thì khi vật cách thấu kính d2=d1' ảnh sẽ cách thấu kính d2'=d1
d1+d1'=d2+d2'=D=1.2m=d1+d2
d1-d2=l=0.72m
Suy ra d1=0.96m và d2=0.24m
Trường hợp ảnh to hơn là vị trí mà khoảng cách đến thấu kính bé hơn do (k=d'/d) chính là trường hợp 2
\(k=\frac{a'}{a}=\frac{d'}{d}=\frac{d_2'}{d_2}=\frac{d_1}{d_2}=4\)
\(a=\frac{a'}{4}=1mm\)
Khoảng vân sẽ là
\(\iota=\frac{\text{λ}D}{a}=0,9mm\)
------>chọn D

Chọn A
Tại vị trí M trên màn, cách vân sáng trung tâm một đoạn 4,4 mm là vân tối thứ 6 tức là: x = 5,5i = 4,4mm => i = 0,8mm.
bước sóng λ của ánh sáng đơn sắc trong thí nghiệm là:
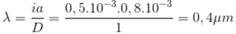
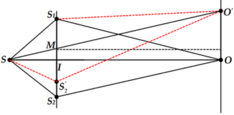

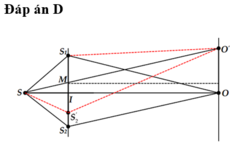
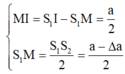
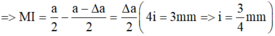
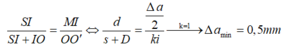
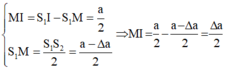
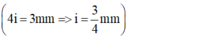
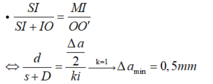
Đáp án D
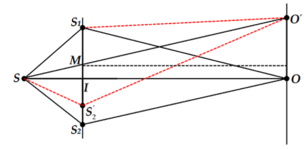
ΔSIM đồng dạng với ΔSOO