Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


Kiến thức áp dụng
Diện tích hình quạt tròn bán kính R, cung nº được tính theo công thức:
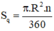

a. gọi M là trung điểm BC
△ ABC vuông tại A có AM là đường trung tuyến
\(\Rightarrow MA=MB=MC=\frac12BC\)
⇒ đường tròn có tâm M đi qua 3 đỉnh của △ ABC
độ dài cạnh BC là:
\(BC=\sqrt{AB^2+AC^2}=\sqrt{15^2+20^2}=25\left(\operatorname{cm}\right)\)
bán kính đường tròn đó là:
\(R=\frac{25}{2}=12,5\left(\operatorname{cm}\right)\)
b. gọi O là giao điểm của 2 đường chéo AC và BD
vì ABCD là hình vuông nên ta có: OA = OB = OC = OD = \(\frac12AC=\frac12BD\)
⇒ đường tròn có tâm O đi qua 4 đỉnh A,B,C,D
độ dài cạnh BD là:
\(BD=\sqrt{AD^2+AB^2}=\sqrt{12^2+12^2}=12\sqrt2\left(\operatorname{cm}\right)\)
bán kính của đường tròn đó là:
\(R=\frac{12\sqrt2}{2}=6\sqrt2\left(\operatorname{cm}\right)\)

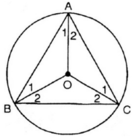
Do ![]()
nên số đo các cung nhỏ AB,BC và AC là:![]()
Suy ra,số đo các cung lớn AB, AC và BC là: 3600 - 1200 = 2400
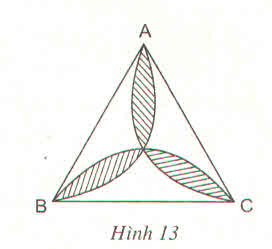



Gọi O là tâm của tam giác đều ABC
Ta có: OA =OB=OC
Vì ABC là tam giác đều nên AO,BO , CO là tia phân giác của góc A , góc B ,góc C trong ∆ OAC ta có: