
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


) Gọi M là trung điểm BC. Lấy điểm D sao cho O là trung điểm CD
Xét Δ BCD có M là trung điểm BC, O là trung điểm CD OM là đường trung bình của Δ BCD
OM=12DB và OM // DB
mà OM⊥BC ( OM là đường trung trực của BC ) DB⊥BC
mà AH⊥BC( AH là đường cao của ΔABC ) AH // DB
Xét ΔABH và ΔBAD có
HABˆ=DBAˆ( 2 góc so le trong do AH // DB )
AB chung
ABHˆ=BADˆ( 2 góc so le trong do AH // DB )
ΔABH=ΔBAD( g-c-g )
AH = BD mà OM=12DB OM=12AH
AH = 2 OM ( đpcm )
b) Gọi G' là giao điển của AM và OH, P là trung điểm G'H, Q là trung điểm G'A
Xét Δ AG'H có P là trung điểm G'H, Q là trung điểm G'A PQ là đường trung bình của \large\Delta AG'H
PQ=12AH và PQ // AH
Do PQ=12AH mà OM=12AH PQ = OM
Do AH // OM ( cùng ⊥BC ) mà PQ // AH PQ // OM
Xét ΔPQG′ và ΔOMG′ có
PQG′ˆ=OMG′ˆ( 2 góc so le trong do PQ // OM)
PQ = OM (c/m trên )
QPG′ˆ=MOG′ˆ ( 2 góc so le trong do PQ //OM )
ΔPQG′=ΔOMG′( g-c-g )
G'Q = G'M và G'P = G'O
Ta có G'Q = G'M mà G′Q=12G′A( Q là trung điểm G'A ) G′M=12G′Amà G'M + G'A = AM
G′A=23AM mà AM là trung tuyến của ΔABC
G' là trọng tâm của ΔABC ,mà G là trọng tâm của ΔABC G′≡ G
mà G′∈OH G∈OH O, H, G thẳng hàng ( đpcm )
Hên xui nghe bạn ^ ^

Bài 7 :
( bạn đạt A = (...) cái biểu thức đấy nhé, tự đặt )
Ta có :
\(\frac{1}{\sqrt{1}}=\frac{1}{1}>\frac{1}{10}=\frac{1}{\sqrt{100}}\)
\(\frac{1}{\sqrt{2}}>\frac{1}{\sqrt{100}}\)
\(\frac{1}{\sqrt{3}}>\frac{1}{\sqrt{100}}\)
\(............\)
\(\frac{1}{\sqrt{100}}=\frac{1}{\sqrt{100}}\)
\(\Rightarrow\)\(A=\frac{1}{\sqrt{1}}+\frac{1}{\sqrt{2}}+\frac{1}{\sqrt{3}}+...+\frac{1}{\sqrt{100}}>\frac{1}{\sqrt{100}}+\frac{1}{\sqrt{100}}+\frac{1}{\sqrt{100}}+...+\frac{1}{\sqrt{100}}\)
\(A>\frac{100}{\sqrt{100}}=\frac{100}{10}=10\)
\(\Rightarrow\)\(A>10\)
Vậy \(A>10\)
Chúc bạn học tốt ~
Bạn làm được mình bài 7 thôi à, mình thấy bạn giỏi lắm mà. Mình có tới mấy chục bài cần giải cơ. Dạo này mình hỏi nhiều vì sắp đi thi.

câu a hơi kì nhỉ , theo mk thì phải là tam giác ABM = tam giác DCM chứ
a) Xét \(\Delta ABM\) và \(\Delta DCM\)có :
AM=DM ( gt )
BM=MC ( gt )
\(\widehat{BMA}=\widehat{DMC}\) ( 2 góc đối đỉnh )
do đó \(\Delta ABM\) = \(\Delta DCM\) ( c.g.c )
b) Vì \(\Delta ABM=\Delta DCM\)( c/m trên )
\(\Rightarrow\widehat{ABM}=\widehat{DCM}\) ( 2 góc tương ứng )
mà 2 góc này ở vị trí so le trong
nên AB // BC

a, xét tam giác AHD và tam giác AHB có : AH hcung
góc AHD = góc AHB = 90
HD = HB (Gt)
=> tam giác HAB = tam giác HAD (2cgv)
=> AD = AB (Đn)
=> tam giác ABD cân tại (Đn)
có góc BAC = 60 (gt)
=> tam giác ABD đều
b, tam giác ABC vuông tại A (gt)
=> góc ABC + góc ACB = 90 (Đl)
góc ABC = 60 (gt)
=> góc ACB = 30 mà tam giác ABC vuông tại A (gt)
=> AB = BC/2 (đl)
có AB = AD = BD do tam giác ABD đều (câu a)
=> AD = BD = BC/2
BD + CB = BC
=> AD = DC = BC/2

Giải
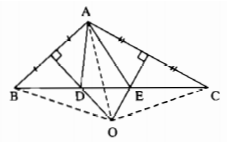
a) D thuộc đường trung trực của AB nên DA = DB (tính chất đường trung trực)
Vậy ∆ADB cân tại D.
E thuộc đường trung trực của AC nên AE = EC (tính chất đường trung trực)
Vậy ∆AEC cân tại A.
b)Vì O là giao điểm ba đường trung trực của ∆ABC nên:
OA = OB = OC
Vậy (O;OA) đi qua ba điểm A, B, C.
Ta có ∠C = 180o - 30o - 60o = 90o
Tam giác ABC vuông tại C nên trực tâm tan giác ABC là điểm C.
Chọn C