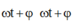Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Hướng dẫn bạn:
- Lực kéo về: \(F=k.x=0,03\sqrt 2\pi\) (không biết có đúng như giả thiết của bạn không)
\(\Rightarrow x =\dfrac{0,03\sqrt 2\pi}{k}=\dfrac{0,03\sqrt 2\pi}{m.\omega^2}=\dfrac{0,03\sqrt 2\pi}{0,01.\omega^2}=\dfrac{3\sqrt 2\pi}{\omega^2}\)
- Áp dụng: \(A^2=x^2+\dfrac{v^2}{\omega^2}\)
\(\Rightarrow 0,05^2=(\dfrac{3\sqrt 2\pi}{\omega^2})^2+\dfrac{(0,4\pi)^2}{\omega^2}\)
Bạn giải pt trên tìm \(\omega \) và suy ra chu kì \(T\) nhé.

\(x=A\sin(\omega t)+A\cos(\omega t)\)
\(=A\sin(\omega t)+A\sin(\omega t+\dfrac{\pi}{2})\)
\(=2A\sin(\omega t+\dfrac{\pi}{4}).\cos \dfrac{\pi}{4}\)
\(=A\sqrt 2\sin(\omega t+\dfrac{\pi}{4})\)
Vậy biên độ dao động là: \(A\sqrt 2\)
Chọn C.

1. B là chu kỳ của dao động.
2. C. Quỹ đạo là đoạn thằng.
3. D. Lực kéo về tỉ lệ với li độ và luôn hướng về vị trí cân bằng. \(\left|F\right|=k\left|x\right|\)
4. Đáp án C sai.
Câu này bạn có thể nhớ giản đồ véc tơ này

Khi đó v sớm pha hơn li độ x 1 góc pi/2
a sớm pha hơn v 1 góc là pi/2
còn a sớm pha hơn x 1 góc pi/2

3 vecto của 3 dao động tạo thành tam giác đều (vì cùng biên độ)
Pha ban đầu của dao động thứ 2 là: \(\phi=-\frac{\pi}{12}-\frac{\pi}{3}=-\frac{5\pi}{12}\left(rad\right)\)

Gia tốc cực đại: \(a_{max}=\omega^2.A=(2\pi.2,5)^2.0,05=12,3m/s^2\)

\(A=l'=\frac{mg}{k}=\frac{g}{\omega^2}\)
\(v_0=A\omega\Rightarrow\frac{g}{\omega}=v_0\Rightarrow\omega=\frac{g}{v_0}\)
\(\Rightarrow A=\frac{g}{\omega^2}=\frac{v^2_0}{g}=6,25\left(cm\right)\)

Độ dời bằng 10% biên độ thì \(|x|=0,1.A\)
A. Do \(a=-\omega^2.x\) nên gia tốc tỉ lệ với li độ, do vậy \(|a|=0,1.A_{max}=10\%.A_{max}\) -->Sai
B. Ta có: \((\dfrac{x}{A})^2+(\dfrac{v}{v_{max}})^2=1\) \(\Rightarrow (0,1)^2+(\dfrac{v}{v_{max}})^2=1\)\(\Rightarrow (\dfrac{v}{v_{max}})^2=0,99\)
\(\Rightarrow \dfrac{v}{v_{max}}=0,995=99,5\%\) -->Đúng.
Vậy chọn B, các ý khác bạn tự thử nhé :)
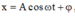

Đáp án C.
Pha dao động :