Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đổi đơn vị: \(\lambda_1=450n m= 0,45 \mu m.\)
\(\lambda_1=600n m= 0,6 \mu m.\)
Hai vân sáng trùng nhau khi \(k_1i_1=k_2i_2 \)
<=> \(\frac{k_1}{k_2}= \frac{i_1}{i_2}=>\frac{k_1}{k_2}= \frac{\lambda_1}{\lambda_2} =\frac{3}{4}\ \ (*)\)
Xét trong đoạn MN nên \(5,5 mm \leq x_s \leq 22mm. \)
<=> \(5,5 mm \leq k_1\frac{\lambda_1 D}{a} \leq 22mm. \)
<=> \(\frac{5,5.a}{\lambda_1 D} \leq k_1\leq \frac{22.a}{\lambda_1 D}\)
Giữ nguyên đơn vị của a = 0,5 mm; D = 2m; \(\lambda_1=0,45 \mu m.\)
<=> \(3,055 \leq k_1 \leq 12,22\)
Kết hợp với (*) ta có \(k_1\) chỉ có thể nhận giá trị : 3x2= 6; 3x3 = 9; 3x4 =12.
Như vậy có 3 vị trí trùng nhau của hai bức xạ trong đoạn MN.

Tịnh tiến màn quan sát lại gần mặt phẳng chưa hai khe 25 cm tức là \(D' = D-0,25.\)
\(i_1 = \frac{\lambda D}{a}\\
i_2 =\frac{\lambda (D-0,25)}{a} \)=> \(\frac{i}{i'}= \frac{D}{D-0,25}= \frac{5}{4}\)
=> \(D = 5.0,25 = 1,25m.\)
=> \(\lambda = \frac{i.a}{D}= 0,48 \mu m.\)
Chú ý là giữ nguyên đơn vị i (mm); a (mm) ; D (m) thì đơn vị bước sóng \(\lambda (\mu m)\).

Chọn đáp án A
? Lời giải:
+ i 2 = λ D 2 a = 750.10 − 6 .2.10 3 2.1 , 5 = 0 , 5 m m

Vị trí hai vân sáng trùng nhau thỏa mãn
\(k_1 i_1 = k_2 i_2 \)
<=> \(k_1 \lambda_1 = k_2 \lambda_2\)
<=> \(\frac{k_1}{k_2}= \frac{\lambda_2}{\lambda_1} = \frac{660}{500}= \frac{33}{25}.\)(*)
Vị trí hai vân sáng trùng nhau đầu tiên (trừ vân trung tâm) ứng với \(k_1;k_2\) nhỏ nhất thỏa mãn (*) tức là \(k_1 = 33; k_2 = 25.\)
Thay \(k_1 =33=> \Delta x_{min}= 33.\frac{500.10^{-3}.1,2}{2}=9,9mm.\)
Với \(\lambda = 500nm = 500,10^{-3}\mu m; a = 2mm; D = 1,2m.\)
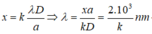
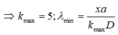
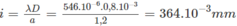



Tại M 1 : x = 1,07mm = 1,07.i/0,364 = 3i
Vậy tại M 1 có vân sáng thứ 3
Tại M 2 : x 2 = 0,91mm = 0,91.i/0,364 = 2,5i = (3 - 1/2)i
Vậy tại M 2 có vân tối thứ 3