Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi cạnh góc vuông là \(x\) thì cạnh huyền là \(a-x\) (điều kiện: \(0< x< a-x\Leftrightarrow0< x< \dfrac{a}{2}\)) và cạnh góc vuông kia là: \(\sqrt{\left(a-x\right)^2-x^2}\).
Diện tích tam giác vuông là:
\(S=\dfrac{1}{2}x\sqrt{\left(a-x\right)^2-x^2}=\dfrac{1}{2}x\sqrt{a^2-2ax}\)
\(S'=\dfrac{1}{2}\sqrt{a^2-2ax}+\dfrac{1}{2}x\dfrac{-a}{\sqrt{a^2-2ax}}\)
\(=\dfrac{1}{2}\dfrac{a^2-3ax}{\sqrt{a^2-2ax}}\)
\(S'=0\Leftrightarrow x=\dfrac{a}{3}\)
S' đổi dấu từ dương sang âm khi x đi qua điểm \(\dfrac{a}{3}\) nên S đạt cực đại tại \(x=\dfrac{a}{3}\).
Khi đó diện tích tam giác vuông là:
\(S\left(\dfrac{a}{3}\right)=\dfrac{1}{2}\dfrac{a}{3}\sqrt{a^2-2a.\dfrac{a}{3}}=\dfrac{a^2\sqrt{3}}{18}\)

Kí hiệu cạnh góc vuông AB là x, 0 < x < a/2
Khi đó, cạnh huyền BC = a – x , cạnh góc vuông kia là:
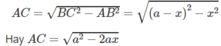
Diện tích tam giác ABC là:
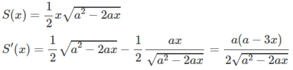
S′(x) = 0 ⇔ x = a/3
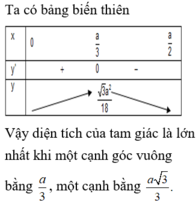
Bảng biến thiên:
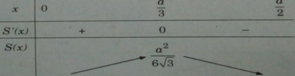
Tam giác có diện tích lớn nhất khi AB = a/3; BC = 2a/3.

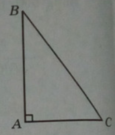
Kí hiệu cạnh góc vuông AB là x, 0 < x < a/2
Khi đó, cạnh huyền BC = a – x , cạnh góc vuông kia là:
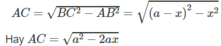
Diện tích tam giác ABC là:
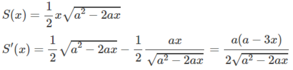
S′(x) = 0 ⇔ x = a/3
Bảng biến thiên:
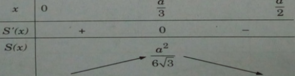
Tam giác có diện tích lớn nhất khi AB = a/3; BC = 2a/3

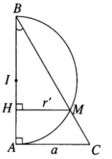
Khi quay xung quanh trục AB, giao điểm M của nửa đường tròn đường kính AB và cạnh CD sẽ tọ nên giao tuyến của mặt nón và mặt cầu.
Vẽ MH ⊥ AB
Ta có:
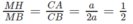
Mặt khác ta có CA 2 = CM.CB nên ta có
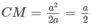
Do đó: BM = CB − CM = 3a/2 và HM = 3a/4



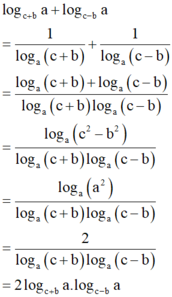




Trong tam giác vuông, góc vuông là góc lớn nhất nên cạnh huyền (đối diện với góc vuông) là cạnh lớn nhất.
Có một nhầm lẫn trong câu hỏi: Trong một tam giác vuông, chiều dài cạnh huyền luôn lớn hơn từng cạnh góc vuông, nhưng không bao giờ lớn hơn tổng chiều dài hai cạnh góc vuông. Thực tế, theo bất đẳng thức tam giác, tổng độ dài hai cạnh bất kỳ luôn lớn hơn cạnh còn lại.
Giải thích đúng:
\(B C^{2} = A B^{2} + A C^{2}\)
\(B C < A B + A C\)
Chứng minh:
Bất đẳng thức tam giác:
Trong tam giác bất kỳ, tổng độ dài hai cạnh luôn lớn hơn cạnh còn lại.
Áp dụng cho tam giác vuông ABC:
\(A B + A C > B C\)So sánh cạnh huyền với từng cạnh góc vuông:
Kết luận:
Nếu bạn muốn, mình có thể giúp bạn chứng minh chi tiết hơn hoặc giải thích thêm!