Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

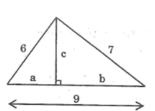
Gọi độ dài đường cao là c, hình chiếu của hai cạnh 6 và 7 trên cạnh có độ dài bằng 9 lần lượt là a và b.
Ta có: a < b (vì 6 < 7)
Theo định lí Pi-ta-go, ta có:
c 2 = 6 2 - a 2 c 2 = 7 2 - b 2
Suy ra:
36 - a 2 = 49 - b 2 ⇔ b 2 - a 2 = 49 - 36
⇔ (b + a)(b – a) = 13 (*)
Mà x + y = 9 nên:
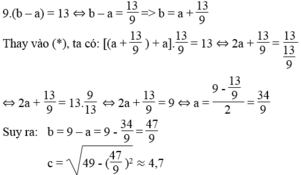

Gọi cạnh dài nhất là a ta có
Ta có √[p(p-a)(p-b)(p-c)]=(a*ha)/2 <=> ha=4*√110 /9 cái còn lại thì áp dụng định lý pytago là ra

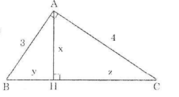
ΔABC vuông tại A có AB = 3, AC = 4 và đường cao AH như trên hình.
Theo định lí Pitago ta có:
![]()
Mặt khác, A B 2 = B H . B C (định lí 1)
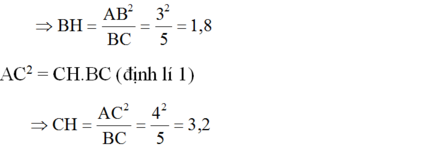
Theo định lí 3 ta có: AH.BC = AB.AC
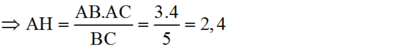

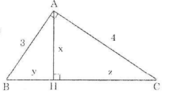
ΔABC vuông tại A có AB = 3, AC = 4 và đường cao AH như trên hình.
Theo định lí Pitago ta có:
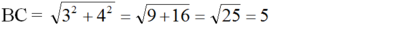
Mặt khác, AB2 = BH.BC (định lí 1)
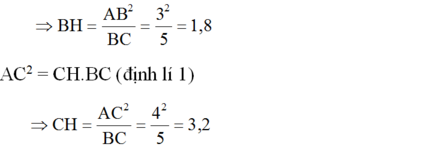
Theo định lí 3 ta có: AH.BC = AB.AC
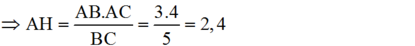

Bài 1:
3 4 x y z
Áp dụng đl pytago ta có:
\(\left(y+z\right)^2=3^2+4^2=9+16=25\)
=> y + z = 5
Áp dụng hệ thức giữa cạnh góc vuông và hình chiếu của nó trên cạnh huyền ta có:
\(3^2=y\left(y+z\right)=5y\)
=>\(y=\frac{3^2}{5}=1,8\)
Có: y + z =5
=>z=5-y=5-1,8=3,2
Áp dụng hên thức liên quan tới đường cao:
\(x^2=y\cdot z=1,8\cdot3,2=\frac{144}{25}\)
=>\(x=\frac{12}{5}\)
Tham khảo: