Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Lời giải:
a. Để $(d)$ đi qua $A(1;0)$ thì:
$y_A=2x_A-m+3$
$\Leftrightarrow 0=2.1-m+3=5-m$
$\Leftrightarrow m=5$
b.
PT hoành độ giao điểm:
$x^2-(2x-m+3)=0$
$\Leftrightarrow x^2-2x+m-3=0(*)$
Để $(P), (d)$ cắt nhau tại 2 điểm pb thì $(*)$ phải có 2 nghiệm pb $x_1,x_2$
Điều này xảy ra khi:
$\Delta'=1-(m-3)>0\Leftrightarrow 4-m>0\Leftrightarrow m< 4$
Áp dụng định lý Viet: $x_1+x_2=2$ và $x_1x_2=m-3$
Khi đó:
$x_1^2-2x_2+x_1x_2=-12$
$\Leftrightarrow x_1^2-(x_1+x_2)x_2+x_1x_2=-12$
$\Leftrightarrow x_1^2-x_2^2=-12$
$\Leftrightarrow (x_1-x_2)(x_1+x_2)=-12$
$\Leftrightarrow x_1-x_2=-6$
$\Rightarrow x_1=-2; x_2=4$
$m-3=x_1x_2=(-2).4=-8$
$\Leftrightarrow m=-5$ (tm)

Phương trình hoành độ giao điểm của (P) và (d) là:
\(x^2=mx+5\)
\(x^2-mx-5=0\)
\(\Delta=m^2+20\)
Vì \(\Delta>0\Rightarrow\) phương trình luôn có 2 nghiệm phân biệt
Vậy đường thẳng (d) và (P) luôn cắt nhau tại 2 điểm phân biệt
Câu tìm m bạn ghi rõ đề ra nhá

Phương trình hoành độ giao điểm:
\(-\dfrac{1}{2}x^2=mx+m-3\Leftrightarrow x^2+2mx+2m-6=0\) (1)
a. Khi \(m=-1\), (1) trở thành:
\(x^2-2x-8=0\Rightarrow\left[{}\begin{matrix}x=4\Rightarrow y=-8\\x=-2\Rightarrow y=-2\end{matrix}\right.\)
Vậy (d) cắt (P) tại 2 điểm có tọa độ là \(\left(4;-8\right)\) ; \(\left(-2;-2\right)\)
b.
\(\Delta'=m^2-2m+6=\left(m+1\right)^2+5>0;\forall m\Rightarrow\left(1\right)\) có 2 nghiệm pb với mọi m
Hay (d) cắt (P) tại 2 điểm pb với mọi m
Theo hệ thức Viet: \(\left\{{}\begin{matrix}x_1+x_2=-2m\\x_1x_2=2m-6\end{matrix}\right.\)
\(x_1^2+x_2^2=14\Leftrightarrow\left(x_1+x_2\right)^2-2x_1x_2=14\)
\(\Leftrightarrow4m^2-2\left(2m-6\right)=14\)
\(\Leftrightarrow4m^2-4m-2=0\Rightarrow m=\dfrac{1\pm\sqrt{3}}{2}\)

Phương trình hoành độ giao điểm là :
\(-x^2=mx+2\)
\(\Leftrightarrow x^2+mx+2=0\)
Lại có : \(\Delta=m^2-8>0\)
Theo định lí Vi - et ta có :
\(\left\{{}\begin{matrix}x1+x2=-m\\x1x2=2\end{matrix}\right.\)
\(\left(x1+1\right)\left(x2+1\right)=0\)
\(\Leftrightarrow x1x2+x1+x1+1=0\)
\(\Leftrightarrow2-m+1=0\Leftrightarrow m=3\)
−x2=mx+2−x2=mx+2
⇔x2+mx+2=0⇔x2+mx+2=0
chúng ta sẽ lại có : Δ=m2−8>0Δ=m2−8>0
Theo định lí Vi - et ta có :
{x1+x2=−mx1x2=2{x1+x2=−mx1x2=2
\(\trái(x1+1\phải)\trái(x2+1\phải)=0\)
⇔x1x2+x1+x1+1=0⇔x1x2+x1+x1+1=0
⇔2−m+1=0⇔m=3

a: Thay x=0 và y=-5 vào (d), ta được:
2(m+1)*0-m^2-4=-5
=>m^2+4=5
=>m=1 hoặc m=-1
b:
PTHĐGĐ là;
x^2-2(m+1)x+m^2+4=0
Δ=(2m+2)^2-4(m^2+4)
=4m^2+8m+4-4m^2-16=8m-12
Để PT có hai nghiệm phân biệt thì 8m-12>0
=>m>3/2
x1+x2=2m+2; x1x2=m^2+4
(2x1-1)(x2^2-2m*x2+m^2+3)=21
=>(2x1-1)[x2^2-x2(2m+2-2)+m^2+4-1]=21
=>(2x1-1)[x2^2+2x2-x2(x1+x2)+x1x2-1]=21
=>(2x1-1)(x2^2+2x2-x1x2-x2^2+x1x2-1]=21
=>(2x1-1)(2x2-1)=21
=>4x1x2-2(x1+x2)+1=21
=>4(m^2+4)-2(2m+2)+1=21
=>4m^2+16-4m-4-20=0
=>4m^2-4m-8=0
=>(m-2)(m+1)=0
=>m=2(nhận) hoặc m=-1(loại)

Xét phương trình hoành độ giao điểm của (d) và (P):
x 2 = m x + 5 ⇔ x 2 − m x − 5 = 0 .
Ta có tích hệ số a c = − 5 < 0 nên phương trình hoành độ giao điểm luôn có 2 nghiệm phân biệt với mọi m hay thẳng (d) cắt parabol (P) tại hai điểm phân biệt với mọi m.
Theo hệ thức Vi-ét ta có x 1 + x 2 = m x 1 x 2 = − 5 Ta có:
x 1 > x 2 ⇔ x 1 2 > x 2 2 ⇔ x 1 2 − x 2 2 > 0 ⇒ x 1 + x 2 x 1 − x 2 > 0
Theo giả thiết: x 1 < x 2 ⇔ x 1 − x 2 < 0 do đó x 1 + x 2 < 0 ⇔ m < 0 .
Vậy thỏa mãn yêu cầu bài toán.

a,bạn thay m = 2 vào (d), lập hoành độ tự tìm nhé
Hoành độ giao điểm (P) ; (d) tm pt
\(x^2-mx-3=0\)
\(\Delta=m^2-4\left(-3\right)=m^2+12>0\)
Vậy pt luôn có 2 nghiệm pb
Theo Vi et \(\left\{{}\begin{matrix}x_1+x_2=m\\x_1x_2=-3\end{matrix}\right.\)
Ta có \(\dfrac{x_1+x_2}{x_1x_2}=\dfrac{3}{2}\)Thay vào ta được
\(\dfrac{m}{-3}=\dfrac{3}{2}\Leftrightarrow m=-\dfrac{9}{2}\)

PTHĐGĐ là;
x^2-6x+m-3=0
Δ=(-6)^2-4(m-3)=36-4m+12=-4m+48
Để PT có hai nghiệm phân biệt thì -4m+48>0
=>m<12
(x1-1)(x2^2-x2(x1+x2-1)+x1x2-1)=2
=>(x1-1)(-x1x2+x2+x1x2-1)=2
=>x1x2-(x1+x2)+1=2
=>m-3-6+1=2
=>m-8=2
=>m=10





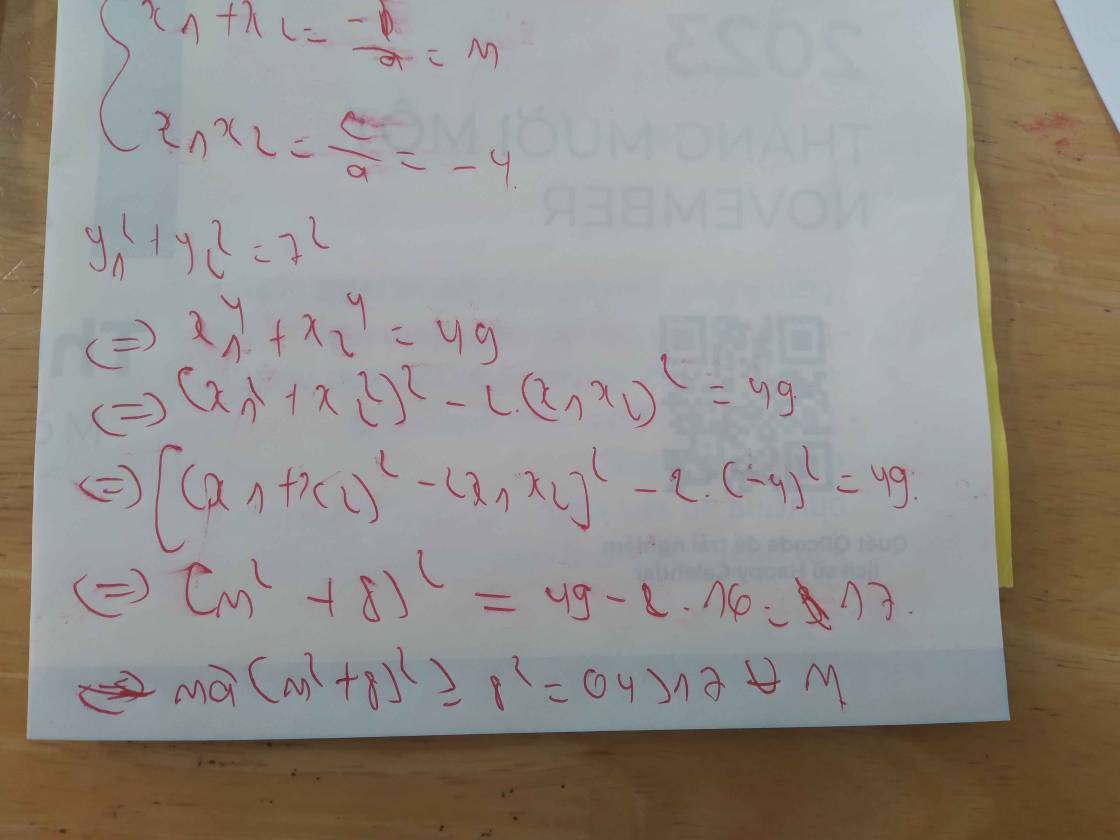

a: Phương trình hoành độ giao điểm là:
\(x^2=mx+m+1\)
=>\(x^2-mx-m-1=0\)
\(\text{Δ}=\left(-m\right)^2-4\cdot1\cdot\left(-m-1\right)=m^2+4m+4=\left(m+2\right)^2\)
Để (d) cắt (P) tại hai điểm phân biệt thì Δ>0
=>m+2<>0
=>m<>-2
b: Theo Vi-et, ta có:
\(\left\{{}\begin{matrix}x_1+x_2=-\dfrac{b}{a}=m\\x_1x_2=\dfrac{c}{a}=-m-1\end{matrix}\right.\)
\(x_1^2\left(x_2+1\right)+x_2^2\left(x_1+1\right)=5\)
=>\(x_1^2\cdot x_2+x_2^2\cdot x_1+\left(x_1^2+x_2^2\right)=5\)
=>\(x_1x_2\left(x_1+x_2\right)+\left(x_1+x_2\right)^2-2x_1x_2=5\)
=>\(m\left(-m-1\right)+m^2-2\left(-m-1\right)=5\)
=>\(-m^2-m+m^2+2m+2=5\)
=>m+2=5
=>m=3(nhận)