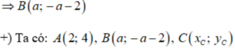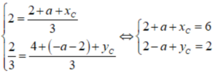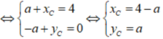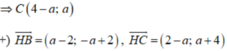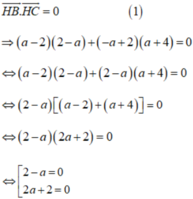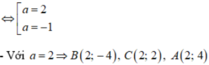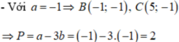Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Tham khảo ở đây nhé!
Trong mặt phẳng tọa độ Oxy cho điểm M(3;1). Giả sử A(a;0) và B(0;b) ( với a, b là các số thực không âm) là 2 điểm sao cho tam giác MAB vuông tại M và có diện tích nhỏ nhất. Tìm a và b
tóm lại đề bài bạn cần làm như sau
bạn tính vecto MA rồi tính vecto MB từ đó tính độ dài MA và MB
=>diện tích tam giác vuông MAB=1/2 MA.MB rồi lập luận thế thôi hết bài
lập luận không khó đâu good luck

Lời giải:
Ta có: \(\overrightarrow{MA}=(a-3;-1); \overrightarrow{MB}=(-3;b-1)\)
Để tam giác MAB vuông tại M thì: \(\overrightarrow{MA}\perp \overrightarrow{MB}\Leftrightarrow \overrightarrow{MA}.\overrightarrow{MB}=0\)
\(\Leftrightarrow -3(a-3)+(-1)(b-1)=0\)
\(\Leftrightarrow 3a+b=10\)
\(2S_{MAB}=|\overrightarrow{MA}|.|\overrightarrow{MB}|=\sqrt{(a-3)^2+1}.\sqrt{9+(b-1)^2}\)
\(=\sqrt{[(a-3)^2+1][9+(10-3a-1)^2}]=3\sqrt{[(a-3)^2+1][1+(a-3)^2]}=3[(a-3)^2+1]\geq 3\)
Vậy diện tích MAB nhỏ nhất khi \(a-3=0\Leftrightarrow a=3\)
\(a=3\Rightarrow b=10-3a=1\)
Vậy...........

Đường tròn \((C)\) tâm \(I(a;b)\) bán kính \(R\)có phương trình
\((x-a)^2+(y-b)^2=R^2.\)
\(∆MAB ⊥ M\) \(\rightarrow \) \(AB\) là đường kính suy ra \(∆\) qua \(I\) do đó:
\(a-b+1=0 (1)\)
Hạ \(MH⊥AB\) có \(MH=d(M, ∆)= \dfrac{|2-1+1|}{\sqrt{2}}={\sqrt{2}} \)
\(S_{ΔMAB}=\dfrac{1}{2}MH×AB \Leftrightarrow 2=\dfrac{1}{2}2R\sqrt{2} \)
\(\Rightarrow R = \sqrt{2} \)
Vì đường tròn qua\(M\) nên (\(2-a)^2+(1-b)^2=2 (2)\)
Ta có hệ :
\(\begin{cases} a-b+1=0\\ (2-a)^2+(1-b)^2=0 \end{cases} \)
Giải hệ \(PT\) ta được: \(a=1;b=2\).
\(\rightarrow \)Vậy \((C) \)có phương trình:\((x-1)^2+(y-2)^2=2\)

a: \(AB=\sqrt{\left[2-\left(-2\right)\right]^2+\left(-1-2\right)^2}=5\)
\(BC=\sqrt{\left(5-2\right)^2+\left(3+1\right)^2}=5\)
Do đó: AB=BC
hay ΔABC cân tại B

a: \(AB=\sqrt{\left(2+2\right)^2+\left(-1-2\right)^2}=5\)
\(BC=\sqrt{3^2+4^2}=5\left(cm\right)\)
Do đó: ΔABC cân tại B