Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
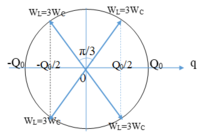
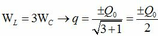
Sử dụng vòng tròn biểu thị dao động điều hòa cho điện tích q, ta thấy thời gian ngắn nhất giữa hai lần liên tiếp năng lượng từ trường bằng ba lần năng lượng điện trường là ∆t = T/6
→ T = 6.10-4 s
Thời gian giữa 3 lần liên tiếp dòng điện trên mạch có giá trị cực đại chính là chu kì T dao động của mạch

Điện tích trên tụ giảm từ cực đại xuống nửa cực đại là \(\dfrac{T}{6}=2.10^-4s\Rightarrow T = 12.10^{-4} s\)
Năng lượng điện giảm từ cực đại xuống nửa cực đại ứng với điện tích giảm từ \(Q_0\) (cực đại) xuống \(\dfrac{Q_0}{\sqrt 2}\)
Biểu diễn bằng véc tơ quay ta thấy véc tơ quay đã quay \(45^0\), ứng với thời gian là: \(\dfrac{T}{8}=1,5.10^{-4}s\)
Chọn A

Ta có : \(\frac{T_{W_{\text{đ}}}}{6}=1,5.10^{-4}\)
\(\Rightarrow\frac{T_q}{6}=\frac{2T_{W_{\text{đ}}}}{6}=3.10^{-4}\)
Vậy chọn D.

Khoảng thời gian liên tiếp giữa hai lần điện trường bằng năng lượng từ trường là \(\frac{T}{4}= \frac{\pi\sqrt{LC}}{2}.\).

Sau khoảng thời gian ngắn nhất \(0,25 \mu s\) năng lượng điện trường và năng lượng từ trường => \(\frac{T}{4}= 0,25 \mu s=> T = 10^{-6}s=> \omega = \frac{2\pi}{T}= 2\pi.10^{6}(rad/s).\)
\(q_0 = \frac{I_0}{\omega} = \frac{2.10^{-8}}{\pi}C.\)
\(W_L=W_C = \frac{0,8}{\pi}.10^{-6}=> q = \pm \frac{q_0}{\sqrt{2}}.\)
Ta có: \(\frac{1}{2}\frac{q_0^2}{2C}=\frac{0,8}{\pi}.10^{-6}=> C = \frac{1,25.10^{-10}}{\pi}F = \frac{125}{\pi}pF.\)
bạn giải đúng rồi nhưng mà đoạn cuối công thức là (1/2)*(q02/C) chứ ko phải là 2C. đáp án là D