Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D.
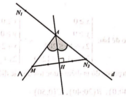
Gọi M’ là điểm đối xứng của M qua đường thẳng d : x 1 = y − 6 − 4 ; z − 6 − 3 .
Gọi H t ; 6 − 4 t ; 6 − 3 t ∈ d là hình chiếu vuông góc của M trên d
Ta có: M H → = t ; t − 4 t ; 3 − 3 t , cho M H → . u d → = 1 + 16 t − 4 + 9 t − 9 = 0 ⇔ t = 1 2 ⇒ H 1 2 ; 4 ; 9 2
Khi đó M ' 1 ; 3 ; 6 suy ra vecto chỉ phương cuả A C → là M ' N → = 0 ; − 2 − 6 = − 2 0 ; 1 ; 3 .

Đáp án C
Δ : x − 1 3 = y + 2 − 2 = z − 3 1 có véc tơ chỉ phương là u → = 3 ; − 2 ; 1
Phương trình mặt phẳng cần tìm đi qua M và vuông góc với đường thẳng
Δ : x − 1 3 = y + 2 − 2 = z − 3 1 nên nhận u → = 3 ; − 2 ; 1 làm véc tơ pháp tuyến có phương trình là:
3
x
−
3
−
2
y
+
1
+
1
z
−
1
=
0
⇔
3
x
−
2
y
+
z
−
12
=
0

Đáp án C.
Mặt phẳng ( P ) : y − z + 2 = 0 có một vecto7 pháp tuyến là n → = ( 0 ; 1 ; − 1 )

Chọn A.
Phương pháp: Đây là bài toán nhận dạng véc tơ chỉ phương của đường thẳng.
Cách giải: Chọn A.


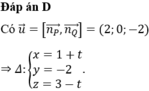


Đáp án A