Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
Vì M ∈ d nên M t + 3 ; − t − 2 ; 2 t + 1 , t ∈ ℝ
Đường thẳng Δ có vtcp u Δ → = − 1 ; 2 ; − 3 .
Đường thẳng d ' : qua M t + 3 ; − t − 2 ; 2 t + 1 vtcp u d ' → = u Δ → = − 1 ; 2 ; − 3
⇒ d ' : x − t + 3 − 1 = y + t + 2 2 = z − 2 t + 1 − 3
M’ là hình chiếu song song của M trên (P)
⇒ M ' = d ' ∩ P ⇒ M ' 5 9 t + 2 ; − 1 9 t ; 2 3 t − 2 .
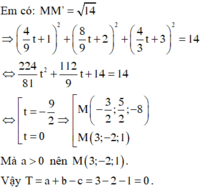

Đáp án B
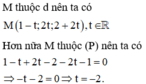
Vậy M(3;−4;−2) là giao điểm của đường thẳng d và mặt phẳng (P).

Đáp án B
Điểm N ∈ d ⇒ N - 2 + 2 t ; 1 + t ; 1 - t mà A là trung điểm của MN ⇒ M 4 - 2 t ; 5 - t ; 3 + t
Mặt khác M = ∆ ∩ P ⇒ M ∈ P ⇒ 2 4 - 2 t - 5 - t + 3 + t - 10 = 0 ⇔ t = - 2
Khi đó M ( 8 ; 7 ; 1 ) , N ( - 6 ; - 1 ; 3 ) ⇒ M N → = - 14 ; - 8 ; 2 ⇒ M N : x + 6 7 = y + 1 4 = z - 3 - 1 .


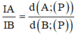
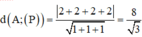
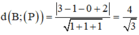
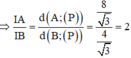


Đáp án C
Do AB có độ dài không đổi nên chu vi tam giác ABC nhỏ nhất khi tổng A C + B C nhỏ nhất.
Do
C ∈ d ⇒ C t ; 0 ; 2 − t ⇒ A C = 2 t − 2 2 + 9 B C = t 2 + 2 − t 2 + 2 = 2 1 − t 2 + 4
Suy ra A C + B C = 2 t − 2 2 2 + 9 + 2 − 2 t 2 + 4 .
Đặt u → = 2 t − 2 2 ; 3 và v → = 2 − 2 t ; 2 . Áp dụng bất đẳng thức u → + v → ≥ u → + v → , dấu “=” xảy ra khi và chỉ khi u → , v → cùng hướng ta được:
2 t − 2 2 2 + 9 + 2 − 2 t 2 + 4 ≥ − 2 2 + 5 2 = 27
Dấu “=” xảy ra ⇔ 2 t − 2 2 2 − 2 t = 3 2 ⇔ t − 2 1 − t = 3 2 ⇔ t = 7 5 . Suy ra C 7 5 ; 0 ; 3 5 .
Vậy C M = 7 5 − 6 5 2 + 0 + 2 2 + 3 5 − 2 2 = 2