Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án B
Ta có M N : x = t y = - 1 - 2 t z = 2 - t .
Gọi H(t;-1-2t;2-t) là hình chiếu vuông góc của K lên MN
Khi đó
H K → = ( t ; - 1 - 2 t ; - t ) . M N → ( - 1 ; 2 ; 1 ) = 0
⇔ t - 2 - 4 t - t = 0 ⇔ t = - 1 3
H K → = ( t ; - 1 - 2 t ; - t ) . M N → ( - 1 ; 2 ; 1 ) = 0
⇒ H - 1 3 ; - 1 3 ; 7 3 . T a c ó d ( K ; ( P ) ) ≤ K H
dấu “=” xảy ra khi KH ⊥ (P)
Khi đó
n → = K H → = - 1 3 ; - 1 3 ; 1 3 = - 1 3 ( 1 ; 1 ; - 1 )

Đáp án B
Gọi H là hình chiếu của O trên (P)
![]()
Dấu bằng xảy ra khi và chỉ khi
![]()
![]()
Mặt phẳng (P) cắt các trục tọa độ lần lượt tại

Vậy thể tích khối chóp OABC là
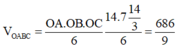

Chọn B
Gọi A(a;0;0), B(0;b;0), C(0;0;c). Ta có phương trình mặt phẳng (P) là: ![]()
Gọi H là hình chiếu của O lên (P). Ta có: d(O, (P)) = OH ≤ OM
Do đó max d(O, (P)) = OM khi và chỉ khi (P) qua M nhận ![]() làm VTPT.
làm VTPT.
Do đó (P) có phương trình:
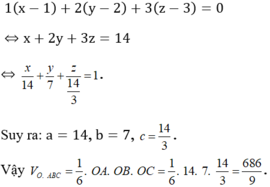

Chọn C

Ta có G(1;0;2), ta tìm hình chiếu của G lên mặt phẳng (P) bằng cách tìm giao điểm của đường thẳng qua G vuông góc với mặt phẳng (P) với mặt phẳng (P).
Phương trình đường thẳng qua điểm G và vuông góc với mặt phẳng (P)
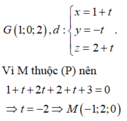

Đáp án D
Phương pháp giải: Xét đẳng thức vectơ, đưa về hình chiếu của điểm trên mặt phẳng
Lời giải:
Gọi M(a;b;c) thỏa mãn đẳng thức vectơ
![]()
=2(1-a;1-b;1-c)+(0-a; 1-b;2-c)+(-2-1;1-b;4-c)=0
![]()
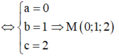
Khi đó
![]()
![]()
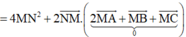
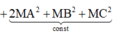
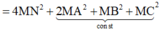
![]()
<=> N là hình chiếu của M trên (P) =>MN ⊥ (P)
Phương trình đường thẳng MN là
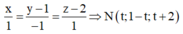
![]()
![]()
![]()

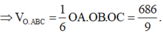
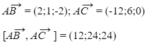



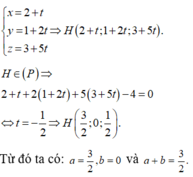
kẻ \(AH\perp BCtạiH\)
\(\overrightarrow{CB}=\left(0;1;-2\right)\)
\(\Rightarrow p+BC:\left\{{}\begin{matrix}x=1\\y=t\\y=2-2t\end{matrix}\right.\\ \Rightarrow H\left(2;t;2-2t\right)\)
\(\Rightarrow\overrightarrow{AH}=\left(1;t-1;1-2t\right)\perp\overrightarrow{CB}\)
\(\Rightarrow0.1+1\left(t-1\right)-2\left(1-2t\right)=0\)
\(\Leftrightarrow t=\dfrac{3}{5}\Rightarrow\overrightarrow{AH}=\left(1;-\dfrac{2}{3};-\dfrac{1}{5}\right)\)
Vì AK≤AH∀(p)
\(\Rightarrow AK_{\max\limits}=AH\Leftrightarrow K\equiv H\)
\(\Rightarrow\overrightarrow{AH}\perp\left(P\right)\Rightarrow\overrightarrow{AH}là1vtpt\)