Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Chọn C
Phương trình tham số của đường thẳng 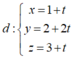
I ∈ d => I (1 + t; 2 + 2t; 3+ t), I ∈ (α) => 1 + t + 2 + 2t – (3 + t) - 2 = 0 ó t = 1 => I (2; 4; 4)
Vectơ chỉ phương của d là ![]()
Vectơ chỉ pháp tuyến của (α) là ![]()
Ta có ![]()
Đường thẳng cần tìm qua điểm I (2; 4; 4), nhận một VTCP là ![]() nên có
nên có
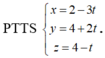
Kiểm tra A (5; 2; 5) ∈ Δ3 (với t = -1) , thấy A (5; 2; 5) thỏa mãn phương trình (*)

Đáp án A
Phương pháp:
Gọi đường thẳng cần tìm là d’
![]()
Tìm tọa độ điểm A.
n d ' → = u d → ; n ( α ) → là 1 VTCP của đường phẳng d’
Cách giải:
Gọi d’ là đường thẳng cần tìm,
![]()
Ta có
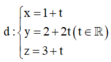
![]()
![]()
![]()
=> A (2;4;4)
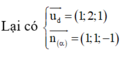
![]()
là một VTCP của d'
Kết hợp với d’ qua A(2;4;4)
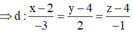
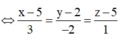

\(\left(1-\dfrac{1}{2}\right)\):\(\left(1-\dfrac{1}{3}\right)\):\(\left(1-\dfrac{1}{4}\right)\):\(\left(1-\dfrac{1}{5}\right)\):\(\left(1-\dfrac{1}{6}\right)\):\(\left(1-\dfrac{1}{7}\right)\)
=\(\left(\dfrac{2-1}{2}\right)\):\(\left(\dfrac{3-1}{3}\right)\):\(\left(\dfrac{4-1}{4}\right)\):\(\left(\dfrac{5-1}{5}\right)\):\(\left(\dfrac{6-1}{6}\right)\)
=\(\dfrac{1}{2}\):\(\dfrac{2}{3}\):\(\dfrac{3}{4}\):\(\dfrac{4}{5}\):\(\dfrac{5}{6}\)
=\(\dfrac{1.\left(3.4.5\right)6}{\left(3.4.5\right)\left(2.2\right)}\)
=\(\dfrac{6}{2.2}=\dfrac{3}{2}\)

Lời giải:
PT hoành độ giao điểm:
\(mx+2m+1-\frac{2x+1}{x+1}=0\Leftrightarrow mx^2+x(3m-1)+2m=0\)
Để hai ĐTHS cắt nhau tại hai điểm $A,B$ thì \(m\neq 0\) và:
\(\Delta=(3m-1)^2-8m^2=m^2-6m+1>0\)
Khi đó áp dụng hệ thức Viete có \(\left\{\begin{matrix} x_1+x_2=\frac{1-3m}{m}\\ x_1x_2=2\end{matrix}\right.\)
Ta có:
\(d(A,Ox)=d(B,Ox)\Leftrightarrow |mx_1+2m+1|=|mx_2+2m+1|\)
TH1: \(mx_1+2m+1=mx_2+2m+1\Leftrightarrow x_1=x_2\)
\(\Rightarrow x_1=x_2=\sqrt{2}\Rightarrow \frac{1-3m}{m}=2\sqrt{2}\) kéo theo \(m=\frac{1}{2\sqrt{2}+3}\) (không thỏa mãn đk của \(\Delta)\)
TH2: \(mx_1+2m+1=-(mx_2+2m+1)\Leftrightarrow m(x_1+x_2)+4m+2=0\)
\(\Leftrightarrow 3+m=0\Rightarrow m=-3\) (t/m)
Vậy $m=-3$

Đáp án B
Phương pháp:
![]()
![]()
![]()
thay tọa độ điểm B vào phương trình ( α ) => 1 phương trình 2 ẩn a, b.
![]()
Sử dụng công thức tính khoảng cách
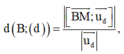
lập được 1 phương trình 2 ẩn chứa a, b.
+) Giải hệ phương trình tìm a,b => Toạ độ điểm B => Độ dài AB.
Dế thấy
![]()
Ta có
![]()
![]()
![]()
Lại có
![]()
Đường thẳng d đi qua M(0;0;-1), có u → = ( 1 ; 2 ; 2 )
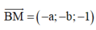
![]()
Do đó
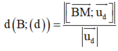
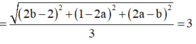
![]()
![]()
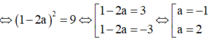
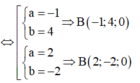
Vậy AB = 7 2

Em chỉ cần chú ý là bán \(\dfrac{1}{2}\) số còn lại mà đang còn dư 18 lít thì số còn lại sau khi bán một nửa là 36 lít. Từ đó suy ra cả thùng chưa bán có tất cả 72 lít

Phương trình \(d_1\) : \(\dfrac{x-1}{1}=\dfrac{y-2}{-1}=\dfrac{z-3}{-1}\) dạng tham số: \(\left\{{}\begin{matrix}x=1+t\\t=2-t\\z=3-t\end{matrix}\right.\)
Gọi A là giao điểm d1 và (P), tọa độ A thỏa mãn:
\(3-t-1=0\Rightarrow t=2\Rightarrow A\left(3;0;1\right)\)
\(\overrightarrow{n_P}=\left(0;0;1\right)\) ; \(\overrightarrow{n_Q}=\left(1;1;1\right)\)
\(\overrightarrow{u_{\Delta}}=\left[\overrightarrow{n_P};\overrightarrow{n_Q}\right]=\left(-1;1;0\right)\)
\(\left[\overrightarrow{u_{\Delta}};\overrightarrow{n_P}\right]=\left(1;1;0\right)\)
Phương trình d: \(\left\{{}\begin{matrix}x=3+t\\y=t\\z=1\end{matrix}\right.\)

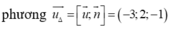
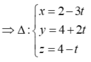



Chọn C
Phương trình tham số của đường thẳng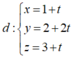
I ∈ d => I (1+t;2+2t;3+t)
I ∈ (α) => 1 + t + 2 + 2t – (3 + t) -2 = 0 ó t = 1 => I (2;4;4).
Đường thẳng cần tìm qua điểm I (2;4;4), nhận một VTCP là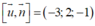 nên có PTTS
nên có PTTS 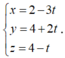
Kiểm tra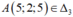 , thấy A (5;2;5) thỏa mãn phương trình (*). Vậy chọn C.
, thấy A (5;2;5) thỏa mãn phương trình (*). Vậy chọn C.