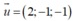Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án A
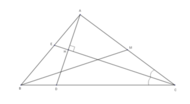
Gọi M là trung điểm của AC, E là chân đường phân giác trong góc C. Ta có:
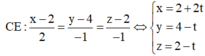
![]()

Vì M thuộc đường trung tuyến kẻ từ B có phương trình
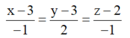
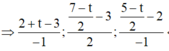
![]()
Kẻ AH vuông góc với CE tại H, cắt BC tại D => Tam giác ACD cân tại C vậy H là trung điểm của AD.
![]()
![]()
vectơ chỉ phương của CE là u → 1 =(2;-1;-1)
![]()
![]()
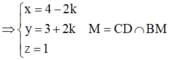
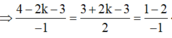
![]()
A B → =(0;2;-2). u → =(m;n;-1) là một vectơ chỉ phương của AB
=> A B → và u → cùng phương.
![]()
![]()

Chọn C
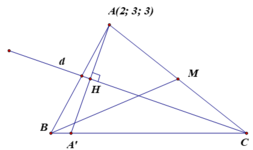
Gọi M là trung điểm của AC. Khi đó M thuộc vào đường trung tuyến kẻ từ B của tam giác ABC.
Giả sử M (3 – t ; 3 + 2t ; 2 – t) ∈ Δ suy ra C (4-2t; 3+4t; 1-2t).
Mà C thuộc và đường phân giác trong d của góc C nên ta có: 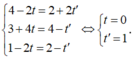
Suy ra C (4; 3; 1).
Gọi H là hình chiếu vuông góc của A trên đường phân giác trong d.
Suy ra H (2+2t';4-t';2-t') ![]()
Ta có ![]() ó 2. 2t'+ (-1) (1-t')+ (-1) (-1-t')=0 ó 4t'-1+t'+1+t'=0 ó t'=0
ó 2. 2t'+ (-1) (1-t')+ (-1) (-1-t')=0 ó 4t'-1+t'+1+t'=0 ó t'=0
=> H (2;4;2).
Gọi A' đối xứng với A qua đường phân giác trong d.
Suy ra A’ ∈ (BC) và A' (2;5;1). Khi đó ![]() là vectơ chỉ phương của đường thẳng BC.
là vectơ chỉ phương của đường thẳng BC.

Đáp án C
Phương pháp:
+) Tam giác ABC có trung tuyến BM và phân giác CD.
+) Tham số hóa tọa độ điểm M là trung điểm của AC, tìm tọa độ điểm C theo tọa độ điểm M.
![]()
+) Tìm tọa độ điểm N đối xứng với M qua CD =>N ∈ BC => Phương trình đường thẳng BC
+) Tìm tọa độ điểm B=BM ∩ BC, khi đó mọi vector cùng phương với AB đều là VTCP của AB.
Cách giải:
Tam giác ABC có trung tuyến BM và phân giác CD.
Gọi M(30t; 3+2t;2-t) ∈ BM là trung điểm của AC ta có
![]()
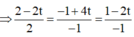
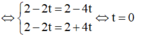
![]()
Gọi H là hình chiếu của M trên CD ta có
![]()
![]()
![]()
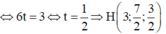
Gọi N là điểm đối xứng với M qua CD => H là trung điểm của MN
![]()
Do CD là phân giác của góc C nên N ∈ BC, do đó phương trình đường thẳng CB là
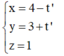
![]()
Xét hệ phương trình
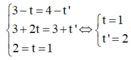
=> B(2;5;1)
![]()
![]()

Chọn A
Gọi M(3-t; 3+2t; 2-t) là trung điểm cạnh AC, khi đó C(4-2t; 3+4t; 1-2t)
Mặt khác C thuộc đường phân giác trong góc C là tam giác nên
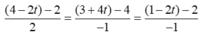
![]()
Gọi A' đối xứng với A qua phân giác trong góc C => A' ∈ CB
Mặt phẳng α qua A và vuông góc với đường phân giác trong góc C:
![]()
![]()
Mặt khác : H là trung điểm AA' nên A'(2;5;1)
Phương trình đường thẳng BC qua A', Clà:
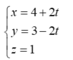
![]()
![]()

Chọn D
Giả sử B (5b ; 0 ; 1 + 4b) ∈ BM, C (4 + 16c ; -2-13c ; 3 + 5c) ∈ CH
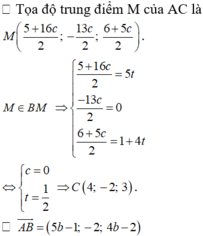
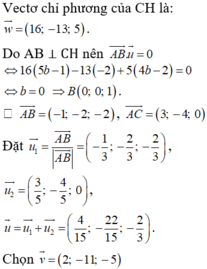
là vectơ chỉ phương của đường phân giác góc A.
Vậy phương trình đường phân giác góc A là: ![]()

A B C H D
Gọi H là chân đường cao từ C
Gọi D là trung điểm của BC \(D \in (d) \) với \((d)\) là đường trung trực của D
Do AB và CH vuông góc với nhau nên AH có vecto pháp tuyến \(\overrightarrow{n_{AB}}=\left(1,1\right)\) mà A(4,-2)
\(\Rightarrow\) Phương trình AB là:
\(x-4+y-(-2)=0 \Leftrightarrow x+y-2=0\)
Do \(B\in AB\) nên \(B(t,2-t)\ t\in \mathbb{R}\)
Do BC vuông góc với (d): 3x+4y-2=0 nên BC có vecto pháp tuyến \(\overrightarrow{n_{BC}}=\left(4,-3\right)\) mà B(t,2-t) thuộc BC
\(\Rightarrow\) Phương trình BC là:
\(4(x-t)-3(y-(2-t))=0 \Leftrightarrow 4x-3y+6-7t=0\)
\(\Rightarrow\) Tọa độ C là nghiệm của hệ:
\(\begin{cases} x-y+2=0\\4x-3y+6-7t=0 \end{cases} \Leftrightarrow \begin{cases} x=7t\\y=7t+2 \end{cases}\)
Do D là trung điểm BC nên tọa độ D là:\(D=(\dfrac{x_B+x_C}{2},\dfrac{y_B+y_C}{2})=(4t,3t+2)\)
Do \(D\in (d):3x+4y-2=0\) nên \(t=\dfrac{-1}{4}\)
\(\Rightarrow\) \(B\left(\dfrac{-1}{4},\dfrac{9}{4}\right),C\left(\dfrac{-7}{4},\dfrac{1}{4}\right)\)

Chọn B
Phương trình tham số của đường phân giác trong góc 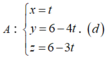
Gọi D là điểm đối xứng với M qua (d). Khi đó D ∈ AC => đường thẳng AC có một vectơ chỉ phương là ![]() .
.
Ta xác định điểm D.
Gọi K là giao điểm MD với (d). Ta có K (t;6-4t;6-3t); ![]()


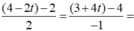

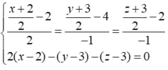
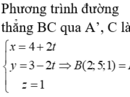
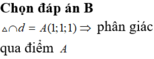
Chọn C
Gọi M là trung điểm AC.
Trung tuyến BM có phương trình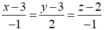 suy ra M (3-m;3+2m;2-m) => C (4 – 2m; 3 + 4m; 1 – 2m).
suy ra M (3-m;3+2m;2-m) => C (4 – 2m; 3 + 4m; 1 – 2m).
Vì C nằm trên đường phân giác trong góc C nên
Gọi A' là điểm đối xứng của A qua phân giác trong góc C, khi đó A' (2+4a;5-2a;1-2a) và A’ ∈ BC.
Véc tơ chỉ phương của đường thẳng chứa phân giác trong góc C là