Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Số cách chọn ra 3 điểm từ 2n điểm đã cho là C 2 n 3 suy ra số mặt phẳng được tạo ra là C 2 n 3 .
Do trong 2n điểm đã cho có n điểm đồng phẳng nên có C n 3 mặt phẳng trùng nhau.
Suy ra số mặt phẳng được tạo thành từ 2n điểm đã cho là C 2 n 3 − C n 3 + 1 .
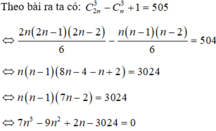

Chọn A
Số tam giác được tạo thành từ 10 điểm là C 10 3 tam giác
Do 4 điểm A 1 , A 2 , A 3 , A 4 thẳng hàng nên số tam giác mất đi là C 10 3
Vậy số tam giác thỏa mãn yêu cầu đề bài là C 10 3 - C 4 3 = 116 tam giác

Đáp án A
Lấy 3 đỉnh trong 10 điểm trên có C 10 3 = 120 cách
Lấy 3 đỉnh trong 4 điểm thẳng hàng có C 4 3 = 4 cách
Do đó, số tam giác cần tính là 120 − 4 = 116

Đáp án D
Phương pháp:
Sử dụng quy tắc nhân.
Cách giải:
Số cách chọn điểm đầu là 2018 cách.
Số cách chọn điểm cuối là 2017 cách (trừ vector không).
Vậy có 2018 × 2017 = 4070306 cách

Đáp án C
Theo đề bài ta có
C n 3 = 2. C n 2 ⇔ n ! 3 ! n − 3 ! = 2. n ! 2 ! n − 2 ! ⇔ 1 6 = 1 n − 2 ⇔ n = 8




Chọn D