Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Kẻ Az//Bx//Dy
=> BAD = BAz + DAz = (180o - ABx) + (180o - ADy) = 30o + 60o = 90o

Hình 1: ta có: \(\hat{NAI}=\hat{AID}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AN//DH
Ta có: \(\hat{AID}=\hat{AKM}\)
mà hai góc này là hai góc ở vị trí đồng vị
nên DH//MK
Ta có: AN//DH
DH//MK
Do đó: AN//DH//MK
Hình 2:
Ta có: \(\hat{N}+\hat{H}=70^0+110^0=180^0\)
mà hai góc này là hai góc ở vị trí trong cùng phía
nên MN//HK

P M N Q O 60 4 2 3 a. Ta có: góc NOQ = POM= 60 ĐỘ
Ta có: MOP+ NOP= 180 độ(do kề bù)
60 + NOP= 180
NOP= 180- 60
Vậy: NOP= 120
Suy ra: MOQ= NOP= 120 độ(do so le trong)

2 góc kề bù trong hình là: góc mOt và tOn
Ta có:
\(\begin{array}{l}\widehat {mOt} + \widehat {tOn} = 180^\circ \\\widehat {mOt} = 180^\circ - \widehat {tOn} = 180^\circ - 60^\circ = 120^\circ \end{array}\)

AB//MN ⇒ góc BAO + góc AON = 180 độ (trong cùng phía)
⇒ góc AON = 180 độ - góc BAO = 180 độ - 120 độ = 60 độ
MN//CD ⇒ góc NOC + góc OCD = 180 độ (trong cùng phía)
=. góc NOC= 180 độ - góc OCD = 180 độ - 140 độ = 40 độ
ta có góc AON = 60 độ, mà góc NOC = 40 độ
vậy ON không phải là phân giác của góc AOC

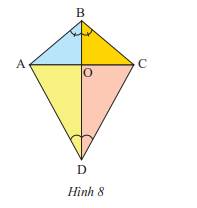
a) Tia BO là tia phân giác của \(\widehat {ABC}\) vì tia BO nằm giữa 2 tia BA và BC, tạo với 2 cạnh BA và BC 2 góc bằng nhau.
Tia DO là tia phân giác của \(\widehat {ADC}\) vì tia DO nằm giữa 2 tia DA và DC, tạo với 2 cạnh DA và DC 2 góc bằng nhau
b) Vì BO là tia phân giác của \(\widehat {ABC}\) nên \(\widehat {ABO} = \widehat {CBO} = \frac{1}{2}.\widehat {ABC} = \frac{1}{2}.100^\circ = 50^\circ \)
Vì DO là tia phân giác của \(\widehat {ADC}\)nên \(\widehat {ADO} = \widehat {CDO} = \frac{1}{2}.\widehat {ADC} = \frac{1}{2}.60^\circ = 30^\circ \)
Vậy \(\widehat {ABO} = 50^\circ ;\widehat {ADO} = 30^\circ \)
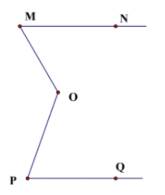





⇒ ∠MOz = ∠OMN = 60⁰
⇒ ∠zOP = ∠MOP - ∠MOz
= 130⁰ - 60⁰
= 70⁰
Để MN // PQ thì MN // Oz
⇒ ∠P = ∠OPQ = ∠POz = 70⁰ (so le trong)