Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho hình thang vuông ABCD có góc A = góc D = 90 độ, AB = AD = CD/2. Qua điểm E thuộc cạnh AB,kẻ đường vuông góc với DE cắt BC tại F. Chứng minh: ED = EF.


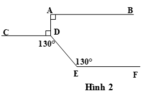
Ta có: A B ⊥ A D ; C D ⊥ A D (gt).
Þ AB // CD (vì cùng vuông góc với AD) (1)
Ta lại có: C D E ^ = E ^ = 130 o (gt)
Þ EF // CD (vì có cặp góc so le trong bằng nhau). (2)
Từ (1) và (2) Þ AB // EF (vì cùng song song với CD).

Sửa đề: Chứng minh MB\(\perp\)MC
Xét ΔABM vuông tại A và ΔDMC vuông tại D có
AB=DM
AM=DC
Do đó: ΔABM=ΔDMC
=>\(\widehat{AMB}=\widehat{DCM}\)
mà \(\widehat{DCM}+\widehat{DMC}=90^0\)
nên \(\widehat{AMB}+\widehat{DMC}=90^0\)
\(\widehat{AMB}+\widehat{BMC}+\widehat{DMC}=180^0\)
=>\(\widehat{BMC}+90^0=180^0\)
=>\(\widehat{BMC}=90^0\)
=>MB\(\perp\)MC


Bạn cho mình xin hình vẽ nha bạn