
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.


a.Đặt \(\dfrac{a}{b}=\dfrac{c}{d}=k\) => \(\left\{{}\begin{matrix}a=bk\\c=dk\end{matrix}\right.\)
Ta có: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(bk\right)^2+\left(dk\right)^2}{b^2+d^2}=\dfrac{k^2\left(b^2+d^2\right)}{b^2+d^2}=k^2\) (1)
\(\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}=\dfrac{\left(bk+dk\right)^2}{\left(b+d\right)^2}=\dfrac{k^2\left(b+d\right)^2}{\left(b+d\right)^2}=k^2\)(2)
Từ (1) và (2) suy ra: \(\dfrac{a^2+c^2}{b^2+d^2}=\dfrac{\left(a+c\right)^2}{\left(b+d\right)^2}\)
b.M = \(\left(1-\dfrac{1}{2^2}\right)\left(1-\dfrac{1}{3^2}\right)\left(1-\dfrac{1}{4^2}\right)...\left(1-\dfrac{1}{50^2}\right)\)
= \(\dfrac{3}{4}.\dfrac{8}{9}.\dfrac{15}{16}...\dfrac{2499}{2500}\)
= \(\dfrac{1.3.2.4.3.5...49.51}{2^2.3^2.4^2...50^2}\)
\(\dfrac{51}{2.50}=\dfrac{51}{100}\)
Lời giải:
a)
Áp dụng tính chất dãy tỉ số bằng nhau:
\(\frac{a}{b}=\frac{c}{d}=\frac{a+c}{b+d}\)
\(\Rightarrow \left(\frac{a}{b}\right)^2=\left(\frac{b}{d}\right)^2=\frac{(a+c)^2}{(b+d)^2}(1)\)
Mặt khác, \(\frac{a}{b}=\frac{c}{d}\Rightarrow \frac{a^2}{b^2}=\frac{c^2}{d^2}=\frac{a^2+c^2}{b^2+d^2}(2)\) (áp dụng tính chất dãy tỉ số bằng nhau)
Từ \((1),(2)\Rightarrow \frac{(a+c)^2}{(b+d)^2}=\frac{a^2+c^2}{b^2+d^2}\)
b) Vì \(1-\frac{1}{2^2};1-\frac{1}{3^2};...;1-\frac{1}{50^2}<1\) nên:
\(\left\{\begin{matrix} \left \{ 1-\frac{1}{2^2} \right \}=1-\frac{1}{2^2}\\ \left \{ 1-\frac{1}{3^2} \right \}=1-\frac{1}{3^2}\\ ....\\ \left \{ 1-\frac{1}{50^2} \right \}=1-\frac{1}{50^2}\end{matrix}\right.\)
\(\Rightarrow M=\left(1-\frac{1}{2^2}\right)\left(1-\frac{1}{3^2}\right)....\left(1-\frac{1}{50^2}\right)\)
\(\Leftrightarrow M=\frac{(2^2-1)(3^2-1)(4^2-1)....(50^2-1)}{(2.3....50)^2}\)
\(\Leftrightarrow M=\frac{[(2-1)(3-1)...(50-1)][(2+1)(3+1)...(50+1)]}{(2.3.4...50)^2}\)
\(\Leftrightarrow M=\frac{(2.3...49)(3.4.5...51)}{(2.3.4...50)^2}=\frac{(2.3.4...49)^2.50.51}{2.(2.3....49)^2.50^2}=\frac{50.51}{2.50^2}=\frac{51}{100}\)

2.Áp dụng tc dãy tỉ số bằng nhau ta có:
\(\frac{a+b+c}{a+b-c}=\frac{a-b+c}{a-b-c}=\frac{a+b+c-a+b-c}{a+b-c-a+b+c}=\frac{2b}{2b}=1\)
\(\Rightarrow a+b+c=a+b-c\)
\(\Rightarrow a+b+c-a-b+c=0\)
\(\Rightarrow2c=0\)
\(\Rightarrow c=0\)
Vậy c=0
BT5: Ta có: f(1)=1.a+b=1 =>a+b=1 (1)
f(2)=2a+b=4 (2)
Trừ (1) cho (2) ta có: 2a+b-a-b=4-1 => a=3
Với a=3 thay vào (1) ta có: 3+b=1 => b=-2
Vậy a=3, b=-2

Xét 2 t.h là ra mà bn : a âm - b dương
a dương -b âm ( loại vì thế k thỏa mãn bài )
minhf cũng làm theo cach này nhưng cô bảo là chưa chắc đã dc điểm![]()

bài 1 : a) oh là tia đối oz \(\Rightarrow\) zoh thẳng hàng
ot là tia đối của tia ox \(\Rightarrow\) xot thẳng hàng
ta có : xoz = \(\dfrac{100}{2}=50^0\) (oz là tia phân giác của góc xoy)
mà xoz = toh (đối đỉnh) \(\Rightarrow\) toh = 500
b) ta có : toh = xoz (đối đỉnh)
mà toh = 400 \(\Rightarrow\) xoz = 400
\(\Rightarrow\) xoy = 40.2 = 800
bạn ơi tớ bảo phần ab bài 1 tớ biết làm rồi tớ muốn cậu có thể giúp tớ bài 2 và bài 3,bài 1 c,d được không
xin cảm ơn các bạn trước!

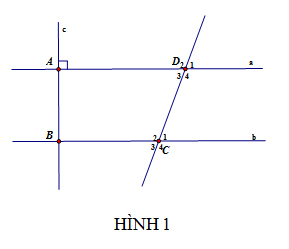
trc hết D1= 70O
a) D1 = D3= 70 (đối đỉnh)
C2 + D3 = 110+70 = 180 ( 2 góc này ở
vị trí trong cùng phía) nên a//b
b) theo a) có a//b
mà c vuông góc với a => c vuong goc voi b

a, Ta có: \(\dfrac{a}{a+b+c}< \dfrac{a}{a+b}< \dfrac{a+c}{a+b+c}\) (1)
\(\dfrac{b}{a+b+c}< \dfrac{b}{b+c}< \dfrac{b+a}{a+b+c}\) (1)
\(\dfrac{c}{a+b+c}< \dfrac{c}{c+a}< \dfrac{c+b}{a+b+c}\) (3)
Từ (1), (2), (3) \(\Rightarrow\dfrac{a}{a+b+c}+\dfrac{b}{a+b+c}+\dfrac{c}{a+b+c}< \dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{c+a}< \dfrac{a+c}{a+b+c}+\dfrac{b+a}{a+b+c}+\dfrac{c+b}{a+b+c}\Rightarrow1< \dfrac{a}{a+b}+\dfrac{b}{b+c}+\dfrac{c}{c+a}< 2\)
Thầy mk hướng dẫn phần a như thế còn phần b mk ko bt lm, chúc p hk tốt ![]()

Với mọi x thuộc R Có (x^2-9)^2 \(\ge\) 0
[y-4] \(\ge\) 0
Suy ra (x^2-9)^2+[y-4] - 1 \(\ge\) -1
Xét A=-1 khi và chỉ khi (x^2-9)^2 và [y-4] đều bằng 0
Tự tính ra
Xin lỗi nhưng vì không biết nên mình phải dùng [ ] thay cho GTTĐ nhé
Xin lỗi nhiều tại mình o tìm được kí hiệu đó

Bài1:
Giải 1 câu các câu sau tương tự
1.A=|x|+1
Với mọi x thì |x|>=0
=>|x|+1 >=1
Hay A>=1
Để A=1 thì |x|=0
=>x=0
Vậy...
Bài2:
1.A=−|x−2|+7
Với mọi x thì −|x−2|nhỏ hơn bằng 0
=>−|x−2|+7 nhỏ hơn bằng 7
Hay A nhỏ hơn bằng 7
Để A=7 thì |x−2|=0
=>x-2=0=>x=2
Các câu sau tương tự
1) \(A=\left|x\right|+1\ge1\forall x\)
\(\Rightarrow GTNN\) của A là 1 khi \(\left|x\right|=0\Leftrightarrow x=0\)
vậy GTNN của A là 1 khi \(x=0\)
2) \(B=\left|x+1\right|-\dfrac{7}{3}\ge-\dfrac{7}{3}\forall x\)
\(\Rightarrow GTNN\) của B là \(-\dfrac{7}{3}\) khi \(\left|x+1\right|=0\Leftrightarrow x+1=0\Leftrightarrow x=-1\)
vậy GTNN của B là \(-\dfrac{7}{3}\) khi \(x=-1\)
3) \(C=\dfrac{2}{5}\left|2x+5\right|-2\ge-2\forall x\)
\(\Rightarrow GTNN\) của C là -2 khi \(\left|2x+5\right|=0\Leftrightarrow2x+5=0\Leftrightarrow2x=-5\Leftrightarrow x=-\dfrac{5}{2}\)
vậy GTNN của C là -2 khi \(x=-\dfrac{5}{2}\)

2) Gọi a,b,c là độ lớn của 3 góc A,B,C
Theo đề bài ta có:
\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}\)
Áp dụng t/c dãy tỉ số bằng nhau:
\(\frac{a}{1}=\frac{b}{2}=\frac{c}{3}=\frac{a+b+c}{1+2+3}=\frac{180}{6}=30\)
\(\Rightarrow\hept{\begin{cases}a=30\\b=60\\c=90\end{cases}}\)
Vậy 3 góc A,B,C lần lượt là 30,60 và 90 độ
1) Áp dụng t/c dãy tỉ số bằng nhau:
\(a=\frac{b}{3}=\frac{c}{4}=\frac{3a-2b+2c}{3-6+8}=\frac{55}{5}=11\)
\(\Rightarrow\hept{\begin{cases}a=11\\b=33\\c=44\end{cases}}\)
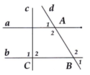
Ta có: A 2 ^ = 150 ° , B 2 ^ = 105 ° => a // b
Mà a ⊥ c => bc => C 1 ^ = C 2 ^ = 90°