Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Cho tam giác abc vuông cân ở a ,m là trung điểm của bc, điểm e nằm giữa m và c.Ke bh,ck vuông với ae (h,k€ae) chứng minh bh=ak.C/m tam giác mbh= tam giác mak.C/m tam giác mhklaf tam giác vuông cân .Vex hình luôn cho mình mình cần gấpkhoang 6 tiênd nữa

Bạn tự vẽ hình nhá!
a) ta có:góc aOx=bOx=góc aOb/2=15002=75015002=750(Ox là p.giác của góc aOb)
góc aOx+góc aOy=180độ(kề bù)
góc aOy=góc aOc+góc cOy
=> góc aOx +góc aOc+góc cOy=180độ
=> góc cOy=180độ-(góc aOx+góc aOc)
=180độ-(75độ+90độ)
=180độ-165độ
=15độ (1)
góc xOb+góc bOy=180độ(kề bù)
góc bOy=góc bOd+góc dOy
=> góc xOb+góc bOd+góc dOy=180độ
=> góc dOy=180độ-(góc xOb+góc bOd)
=180độ-(75độ+90độ)
=180độ-165độ
=15độ (2)
từ (1) và (2)=> góc dOy=góc cOy(=15độ)
=> Oy là p.giác của góc dOc
b)góc xOc=góc aOx+góc aOc
=75độ+90độ
=165độ
góc yOb=góc yOd+góc dOb
=15độ+90độ
=105độ
=> góc xoc>góc yob(165độ>105độ)
Xong rồi , k mình nhé
a, Ox và OC thuộc hai nửa mặt phẳng đối nhau bờ OA nên tia OA nằm giữa hai tia Ox,OC do đó :
\(\widehat{xOC}=\widehat{xOA}+\widehat{AOC}=75^0+90^0=165^0\)
Ox,Oy là hai tia đối nhau nên \(\widehat{xOC}+\widehat{COy}=180^0\)
\(\Leftrightarrow165^0+\widehat{COy}=180^0\Leftrightarrow\widehat{COy}=15^0\)
Tương tự ta có : \(\widehat{xOD}\)= 1650 , \(\widehat{DOy}=15^0\)
Từ đó suy ra Oy là tia phân giác của góc COD
b, Phần so sánh dễ,tự làm
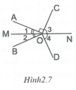
Vì M O N ^ là góc bẹt nên O 1 ^ + O 3 ^ + A O C ^ = 180 ° (1)
O 2 ^ + O 4 ^ + B O D ^ = 180 ° (2)
Mặt khác, O 1 ^ = O 2 ^ ; O 3 ^ = O 4 ^ (đề bài cho) nên từ (1) và (2) suy ra A O C ^ = B O D ^ .
Vì A O C ^ = 90 ° nên B O D ^ = 90 ° ⇒ O B ⊥ O D