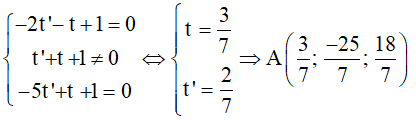Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) Phương trình đường thẳng d có dạng: , với t ∈ R.
b) Đường thẳng d vuông góc với mặt phẳng (α): x + y - z + 5 = 0 nên có vectơ chỉ phương
(1 ; 1 ; -1) vì
là vectơ pháp tuyến của (α).
Do vậy phương trình tham số của d có dạng:
c) Vectơ (2 ; 3 ; 4) là vectơ chỉ phương của ∆. Vì d // ∆ nên
cùng là vectơ chỉ phương của d. Phương trình tham số của d có dạng:
d) Đường thẳng d đi qua hai điểm P(1 ; 2 ; 3) và Q(5 ; 4 ; 4) có vectơ chỉ phương
(4 ; 2 ; -1) nên phương trình tham số có dạng:

a) Gọi \(\overrightarrow{u}\left(1;-2;-1\right)\) là vectơ chỉ phương của d, giả sử \(\overrightarrow{v}\left(a;b;c\right)\) là 

a) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
3(12 + 4t) +5(9 + 3t) - (1 + t) = 0
⇔ 26t + 78 = 0 ⇔ t = -3.
Tức là d ∩ (α) = M(0 ; 0 ; -2).
Trong trường hợp này d cắt (α) tại điểm M.
b) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
(1 + t) + 3.(2 - t) + (1 + 2t) + 1 = 0
⇔ 0.t + t = 9, phương trình vô nghiệm.
Chứng tỏ d và (α) không cắt nhau., ta có d // (α).
c) Thay các tọa độ x ; y ; z trong phương trình tham số của d vào phương trình (α) ta có:
(1 + 1) + (1+ 2t) + (2 - 3t) - 4 = 0
⇔ 0t + 0 = 0,phương trình này có vô số nghiệm, chứng tỏ d ⊂ (α) .