Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi số quýt ban đầu ở mỗi rổ là x (quả)
Muốn lấy 30 quả ở rổ thứ nhất đưa sang rổ thứ hai thì số quả ở mỗi rổ lúc đầu phải nhiều hơn 30 quả hay x > 30.
Khi đó rổ thứ nhất còn x – 30 quả; rổ thứ hai có x + 30 quả.
Vì số quả ở rổ thứ hai bằng 1/3 bình phương số quả còn lại ở rổ thứ nhất nên ta có phương trình:
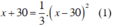
Giải phương trình (1):
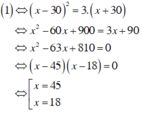
Vì x > 30 nên x = 45 thỏa mãn.
Vậy ban đầu mỗi rổ có 45 quả cam.

Khối lượng muối tinh khiết ( muối không chứa nước) trong 15kg muối là:
15: 100.12 = 1,8 (kg)
Khối lượng nước muối khi ta đổ thêm 3kg nước tinh khiết là:
15 + 3 = 18 (kg)
Vì khối lượng muối tinh khiết không đổi nên số lượng muối chiếm số % trong nước muối lúc sau là:
1,8 : 18 .100 = 10%
Vậy lúc này ta được 1 bình chứa 10% muối
Chúc bn hk tốt ^^

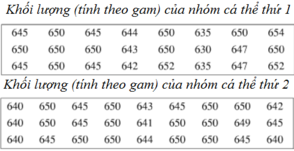
a) Bảng phân bố tần số và tần suất:
| Nhóm cá thứ I | Tần số | Tần suất |
|---|---|---|
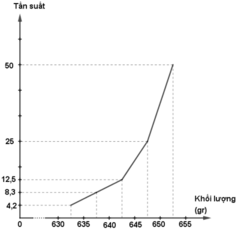
| [630;635) | 1 | 4,2% |
| [635;640) | 2 | 8,3% |
| [640;645) | 3 | 12,5% |
| [645;650) | 6 | 25% |
| [650;655] | 12 | 50% |
| Cộng | 24 | 100% |
b) Bảng phân bố tần số và tần suất:
| Nhóm cá thứ I | Tần số | Tần suất |
|---|---|---|
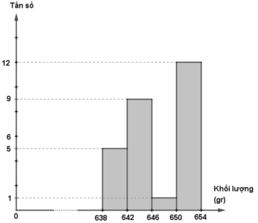
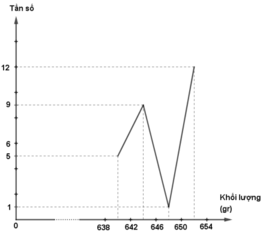
| [638;642) | 5 | 18,52% |
| [642;646) | 9 | 33,33% |
| [646;650) | 1 | 3,7% |
| [650;654) | 12 | 44,45% |
| Cộng | 27 | 100% |
c) Biểu đồ tần suất hình cột:
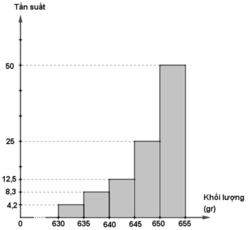
- Đường gấp khúc tần suất
d) Biểu đồ tần số
- Đường gấp khúc tần số
e) * Xét bảng phân bố ở câu a)
- Số trung bình:
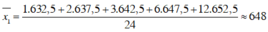
- Phương sai:
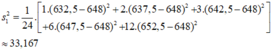
- Độ lệch chuẩn:
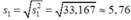
* Xét bảng phân bố ở câu b):
- Số trung bình:
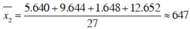
- Phương sai:
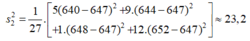
- Độ lệch chuẩn:
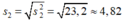
Nhận thấy s2 < s1 nên nhóm cá thứ hai có khối lượng đồng đều hơn.

Bài 1:
Giải:
Vì 2 số chẵn liên tiếp hơn kém nhau 2 đơn vị nên số chẵn bé kém hơn số chẵn lớn 2 đơn vị.
Số chẵn bé là :
( 86 - 2 ) : 2 = 42
Số chẵn lớn là:
86 - 42 = 44
Đáp số: số chẵn bé: 42
số chẵn lớn: 44
Bài 2:
Giải:
Tổng số tuổi của các thành viên trong đội bóng đó là:
11 x 22 = 242 ( tuổi )
Nếu không tính thủ môn thì tổng số tuổi của các thành viên còn lại là:
21 x 10 = 210 ( tuổi )
Tuổi của thủ môn là:
242 - 210 = 32 ( tuổi )
Đáp số: 32 tuổi
1
trung bình cộng 2 số chẵn đó là:
86:2=43
vậy số lớn là 43+1=44
số bé là 43-1=42
2
tổng số tuổi của thủ môn và các cầu thủ là:
22x11=242(tuổi)
tổng số tuổi của 10 cầu thủ là:
10x22=220(tuổi)
tuổi của thủ môn là:
242-220=24(tuổi)
3
a)luợng mật ong còn ở trại là:
135.62,5%=