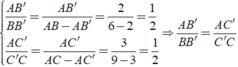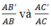Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

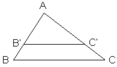
Áp dụng hệ quả trên ta có: Δ ABC, B'C'//BC; B' ∈ AB, C' ∈ AC
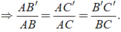
Khi đó ta có: AB'/AB = AC'/AC ⇔ 2/8 = 3/AC ⇒ AC = (3.8)/2 = 12( cm )

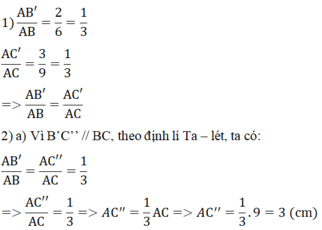
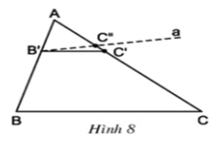
b) Trên đoạn thẳng AC ta có: AC’= AC’’= 3 cm nên
Khi đó, hai đường thẳng BC và B’C’ song song với nhau.

a, xét tam giác AMN và tam giác ABC có:
\(\frac{AM}{AB}=\frac{4}{6}=\frac{2}{3}\)
\(\frac{AN}{NC}=\frac{6}{9}=\frac{2}{3}\)
=> MN // BC( hệ quả định lí ta -let)
b,vì MN// BC=> \(\frac{AM}{MB}=\frac{MN}{BC}\)hay \(\frac{4}{6}=\frac{MN}{12}\Rightarrow MN=4.12:6=8cm\)

Theo định lý Ta - let ta có:
\(\dfrac{AB'}{AB}=\dfrac{AC'}{AC}\)
\(\Leftrightarrow\dfrac{4}{6}=\dfrac{3}{AC}\)
\(\Rightarrow\dfrac{2}{3}=\dfrac{1}{AC}\)
\(\Rightarrow2AC=3\)
\(\Rightarrow AC=\dfrac{2}{3}\)

a, ta có
BC^2=5^2=25
AB^2+AC^2=3^2+4^2=9+16=25
=>AB^2+AC^2=BC^2
=> tam giác ABC vuông tại A
b.
Dx vuông góc với BC
=> góc BDH=90 độ
xét tam giác HBA và tam giác HBD có
BA=BD(gt)
HB cạnh chung
góc HAB=góc HDB= 90 độ
=> tam giác HBA= tam giác HBD(cạnh huyền- cạnh góc vuông)
=> góc HBA=góc HBD(hai góc tương ứng)
=> BH là phân giác góc ABD

nối D với E vì DA = 2 cm => D là trung điểm của AB ( AB = 4cm)
vì AE = 3 cm => E là trung điêm của AC ( AC= 6 cm)
XÉT tam giác ABC
D là trung điểm của AB
E là trung điểm của AC
=> DE là đường trung bình của tam giác
=> DE // BC ( đường trung bình // với đáy bằng nửa đáy)