Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
^_^
\(x=A\sin(\omega t)+A\cos(\omega t)\)
\(=A\sin(\omega t)+A\sin(\omega t+\dfrac{\pi}{2})\)
\(=2A\sin(\omega t+\dfrac{\pi}{4}).\cos \dfrac{\pi}{4}\)
\(=A\sqrt 2\sin(\omega t+\dfrac{\pi}{4})\)
Vậy biên độ dao động là: \(A\sqrt 2\)
Chọn C.
Có: \(L=CR^2=Cr^2\Rightarrow R^2=r^2=Z_LZ_C,URC=\sqrt{3U}_{Lr}\Leftrightarrow Z^2_{RC}=3Z^2_{Lr}\Leftrightarrow R^2+Z^2_C=3\left(Z^2_L+R^2\right)\)
\(\Leftrightarrow-3Z^2_L+Z^2_C=2R^2\) (*) \(R^2=Z_LZ_C\) (**)
Từ (*) và (**) có: \(Z_L=\frac{R}{\sqrt{3}};Z_C=\sqrt{3}R\Rightarrow Z=\sqrt{\left(R+r\right)^2Z^2_{LC}}=\frac{4R}{\sqrt{3}}\Rightarrow\cos\phi=\frac{R+r}{Z}=\frac{\sqrt{3}}{2}\approx0,866\)
A đúng
Nhiệt lượng tỏa ra: \(Q=I^2Rt\)
\(\Rightarrow9.10^5=I^2.10.30.60\)
\(\Rightarrow I=5\)
Biên độ dòng điện \(I_0=5\sqrt{2}\)(A)
Bạn Trần Hoàng Sơn có chút nhầm lẫn, ta tìm đc \(I=5\sqrt{2}A\)
\(\Rightarrow I_0=\sqrt{2}I=10A\)
Chọn C.
Ta có:
Con lắc thực hiện 100 dao động hết 31,4 (s)
Lại có gốc thời gian là lúc quả cầu có li độ 2cm và đang chuyển động theo chiều dương của trục tọa độ với vận tốc có độ lớn
và
Đáp án C
Phương pháp: Sử dụng lí thuyết về các tia phóng xạ ̣
Tia α cóbản chất là hạt nhân nguyên tử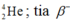
là các eletron, kí hiệu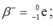
là sóng điện từ có bước sóng rất ngắn, là hạt photon có năng lượng cao
Sử dụng lí thuyết về các tia phóng xạ
Cách giải: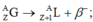
Chọn C