Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
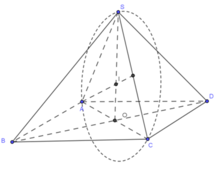
Gọi d = x ⇒ I O 2 = x − 9 2 .
Có O C = I C 2 − I O 2
= 9 2 − x − 9 2 = 18 x − x 2
⇒ A C = B D = 2 18 x − x 2
Vậy P = S O . S A B C D = x . 1 2 A C . B D
= 2 x . 18 x − x 2 = 2 x 2 18 − x
Có 36 = x + x + 2 18 − x
≥ 3 2 x 2 . 18 − x 3
⇒ x 2 18 − x ≤ 864.
Vậy P đạt giá trị lớn nhất khi x = 2 18 − x ⇔ x = 12 .

Chọn C.
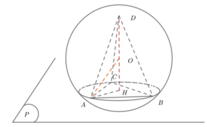
Phương pháp: Tìm vị trí điểm D để thể tích ABCD lớn nhất.

Đáp án C
Gọi chiều cao của hình chóp là 9 + x , x ≥ 0 , cạnh của hình chóp là a , a ≤ 9 2
Diện tích đáy của hình chóp là: V = 1 3 .2 81 − x 2 9 + x = 2 3 9 − x = 2 3 9 − x 9 + x 9 + x
= 1 3 18 − 2 x 9 + x 9 + x = 1 3 ≤ 1 3 18 − 2 x + 9 + x + 9 + x 3 3 = 1 3 .12 3 = 576


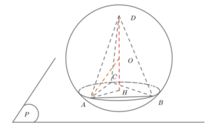
Đáp án B
Ta có: R = S A 2 2 S O = 9
Suy ra S O 2 + O A 2 S O = 18
Mặt khác V S . A B C D = 1 3 S O . S A B C D = 1 3 S O . A C 2 2 = 2 3 S O . O A 2
= 2 3 S O . 18 S O − S O 2 . đặt S O = t 0 < t < 18 , xét hàm số
f t = 2 3 t 2 18 − t = 8 3 . t 2 . t 2 18 − t ≤ 8 3 t + 18 − t 3 3 = 576
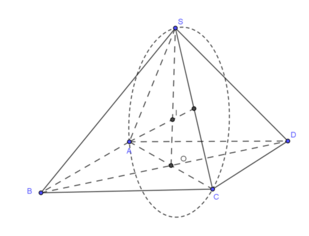
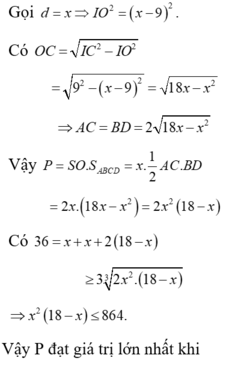



Xét tứ giác ABCD nội tiếp trong đường tròn (O;R).Gọi H và K là chân các đường vuông góc kẻ từ B và D đến AC.Ta có
S(ABCD) = S(ABC) + S(ADC) = (1/2) AC.BH + (1/2) AC.DK = (1/2)AC (BH + DK)
BH + DK chính là tổng khoảng cách từ 2 điểm thuộc đường tròn ở 2 phía của 1 dây cung đến dây cung đó, và tổng đó nhỏ hơn hoặc bằng 2R
Còn AC là 1 dây cung nên AC cũng không lớn hơn 2R
Vậy S(ABCD) = (1/2) AC (BH + DK) <= (1/2). 2R. 2R = 2R^2
Dấu bằng xảy ra khi AC và BD là đường kính, tức ABCD là hình vuông.
Vậy tứ giác nội tiếp (O;R) có diện tích lớn nhất là hình vuông
Khi đó S(hình vuông ABCD) = 2R^2
-st-