Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

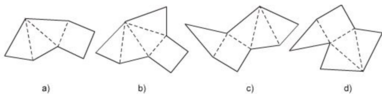
Hình a, khi gấp lại thì không được một hình chóp đều vì đáy là tứ giác đều nhưng chỉ có ba mặt bên thay vì phải có 4 mặt bên.
Hình b, c khi gấp lại thì được một hình chóp tứ giác đều.
Hình d, khi gấp lại thì không được một hình chóp tứ giác đều vì ở trên cùng một cạnh đáy có đến 2 mặt bên còn trên một cạnh đáy thì không có mặt bên nào.

Hình a, khi gấp lại thì không được một hình chóp đều vì đáy là tứ giác đều nhưng chỉ có ba mặt bên thay vì phải có 4 mặt bên.
Hình b, c khi gấp lại thì được một hình chóp tứ giác đều.
Hình d, khi gấp lại thì không được một hình chóp tứ giác đều vì ở trên cùng một cạnh đáy có đến 2 mặt bên còn trên một cạnh đáy thì không có mặt bên nào.

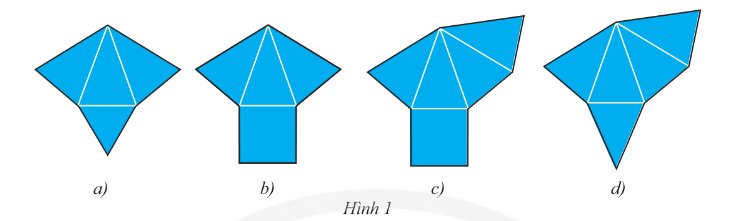
1a gấp được thành hình chóp tam giác đều
1c gấp được thành hình chóp tứ giác đều

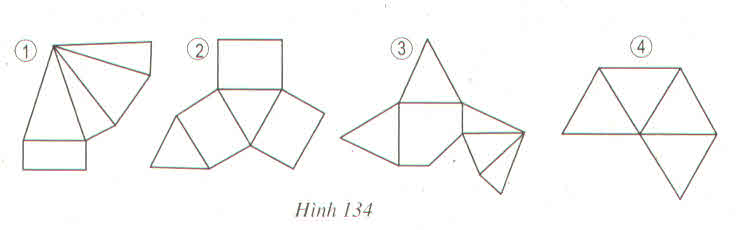
Hình 1: Khi gấp lại không được hình chóp đều vì hình chóp thu được có đáy là hình chữ nhật. Không là đa giác đều.
Hình 2: Khi gấp lại ta được hình lăng trụ đứng đáy tam giác đều. Không phải là hình chóp đều
Hình 3: Khi gấp lại không được hình chop đều vì hình chóp thu được có đáy là hình ngũ giác không phải là ngũ giác đều.
Hình 4: Khi gấp lại không được hình chóp đều vì hình thu được là hình chóp đều thiếu một mặt đáy và dư một mặt bên.
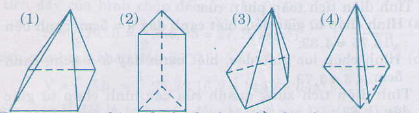
Hình 1: Khi gấp lại không được hình chóp đều vì hình chóp thu được có đáy là hình chữ nhật. Không là đa giác đều.
Hình 2: Khi gấp lại ta được hình lăng trụ đứng đáy tam giác đều. Không phải là hình chóp đều
Hình 3: Khi gấp lại không được hình chop đều vì hình chóp thu được có đáy là hình ngũ giác không phải là ngũ giác đều.
Hình 4: Khi gấp lại không được hình chóp đều vì hình thu được là hình chóp đều thiếu một mặt đáy và dư một mặt bên.

Tấm bìa hình 11b, 11c gấp theo đường màu đỏ thì được hình chóp tứ giác đều

Bài 64 (trang 100 SGK Toán 8 Tập 1): Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình 91. Chứng minh rằng EFGH là hình chữ nhật.
Theo giả thiết ABCD là hình bình hành nên ta có:
ˆDAB=ˆDCB,ˆADC=ˆABC (1)
Theo định lí tổng các góc của một tứ giác ta có:
ˆDAB+ˆDCB+ˆADC+ˆABC=360o (2)
Từ (1) và (2) ⇒ˆDAB+ˆABC=360o/2=180o
Vì AG là tia phân giác ˆDAB (giả thiết)
⇒⇒ ˆBAG=1/2ˆDAB (tính chất tia phân giác)
Vì BG là tia phân giác ˆABC (giả thiết)
⇒⇒ ˆABG=1/2ˆABC
Do đó: ˆBAG+ˆABG=1/2(ˆDAB+ˆABC)=1/2.1800=90o
Xét ΔAGB= có:
ˆBAG+ˆABG=90o (3)
Áp dụng định lí tổng ba góc trong một tam giác vào tam giác AGBAGB ta có:
ˆBAG+ˆABG+ˆAGB=180o (4)
Từ (3) và (4) ⇒ˆAGB=90o
Chứng minh tương tự ta được: ˆDEC=ˆEHG=90o
Tứ giác EFGH có ba góc vuông nên là hình chữ nhật (dấu hiệu nhận biết hình chữ nhật)
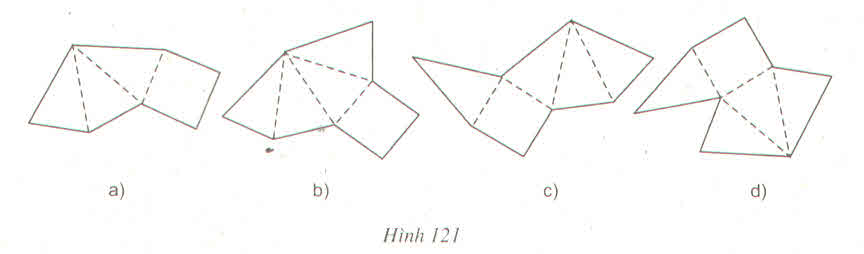
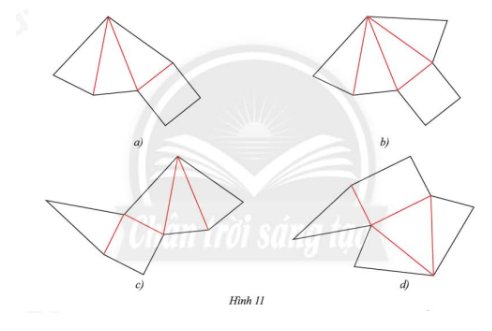

Hình a khi gấp lại thì không được một hình chóp đều vì đáy là tứ giác đều nhưng chỉ có ba mặt bên thay vì phải có 4 mặt bên.
Hình b, c khi gấp lại thì được một hình chóp tứ giác đều.
Hình d khi gấp lại thì không được một hình chóp tứ giác đều vì ở trên cùng một cạnh đáy có đến 2 mặt bên còn trên một cạnh đáy thì không có mặt bên nào.