Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

a) \(\dfrac{3}{8}\) và \(\dfrac{5}{27}\)
Mẫu số chung là 216
Quy đồng:
\(\dfrac{3.27}{8.27}\)=\(\dfrac{81}{216}\) ; \(\dfrac{5.8}{27.8}\)=\(\dfrac{40}{216}\)
b)\(\dfrac{-2}{9}\) và \(\dfrac{4}{25}\)
Mẫu số chung là:225
Quy đồng:
\(\dfrac{-2.25}{9.25}\)=\(\dfrac{-50}{225}\) ; \(\dfrac{4.9}{25.9}\)=\(\dfrac{36}{225}\)
c)\(\dfrac{1}{15}\) và -6
Mẫu số chung là 15
Quy đồng:
\(\dfrac{1}{15}\) ;\(\dfrac{-6.15}{15}\)=\(\dfrac{-90}{15}\)

a. \(\dfrac{-3}{5}\)
b. \(\dfrac{-2}{3}\) c. \(\dfrac{4}{39}\) d. \(\dfrac{26}{45}\)

\(a,\dfrac{7}{35},\dfrac{18}{54},\dfrac{-15}{125},\dfrac{-4}{25}\)
Các thừa số đã tối giản : \(\dfrac{-4}{25}\)
\(\dfrac{7}{35}=\dfrac{7:7}{35:7}=\dfrac{1}{5}\) , \(\dfrac{18}{54}=\dfrac{18:18}{54:18}=\dfrac{1}{3}\)
\(\dfrac{-15}{125}=\dfrac{-15:5}{125:5}=\dfrac{-3}{25}\)
\(b,\dfrac{27}{45},\dfrac{21}{28},\dfrac{8}{14},\dfrac{18}{-60},\dfrac{-270}{360}\)
Các thừa số đã tối giản là : ko có
\(\dfrac{27}{45}=\dfrac{27:9}{45:9}=\dfrac{3}{5}\) , \(\dfrac{21}{28}=\dfrac{21:7}{28:7}=\dfrac{3}{4}\)
\(\dfrac{8}{14}\)\(=\dfrac{8:2}{14:2}=\dfrac{4}{7}\) , \(\dfrac{18}{-60}=\dfrac{18:6}{-60:6}=\dfrac{3}{-10}=\dfrac{-3}{10}\)
\(\dfrac{-270}{360}=\dfrac{-270:90}{360:90}=\dfrac{-3}{4}\)
\(c,\dfrac{3.4+3.7}{6.5+9}\) = \(\dfrac{3.\left(4+7\right)}{30+9}\) = \(\dfrac{3.11}{39}\) = \(\dfrac{3.11}{3.13}=\dfrac{11}{13}\)
\(\dfrac{-63}{81},\dfrac{9.6}{9.35},\dfrac{7.2+8}{2.14.5}\)
Các p/s đã tối giản : ko có
\(\dfrac{-63}{81}=\dfrac{-63:9}{81:9}=\dfrac{-7}{9}\) , \(\dfrac{9.6}{9.35}=\dfrac{6}{35}\)
\(\dfrac{7.2+8}{2.14.5}=\dfrac{14+8}{28.5}=\dfrac{22}{140}=\dfrac{11}{70}\)

a) \(\dfrac{1}{6};\dfrac{1}{3};\dfrac{1}{2};...\)
\(\Rightarrow\dfrac{1}{6};\dfrac{2}{6};\dfrac{3}{6};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{4}{6}\)
b) \(\dfrac{1}{8};\dfrac{5}{24};\dfrac{7}{24};...\)
\(\Rightarrow\dfrac{3}{24};\dfrac{5}{24};\dfrac{7}{24};...\)
Dãy có quy luật tăng dần lên 2 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{9}{24}\)
c) \(\dfrac{1}{5};\dfrac{1}{4};\dfrac{1}{3};...\)
\(\dfrac{4}{20};\dfrac{5}{20};\dfrac{6}{20};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{7}{20}\)
d) \(\dfrac{4}{15};\dfrac{3}{10};\dfrac{1}{3};...\)
\(\Rightarrow\dfrac{8}{30};\dfrac{9}{30};\dfrac{11}{30};...\)
Dãy có quy luật tăng dần lên 1 đơn vị ở tử số
\(\Rightarrow\) Số tiếp theo của dãy là: \(\dfrac{12}{30}\)

Ta có \(\dfrac{a}{b}=\dfrac{18}{27}=\dfrac{2}{3}\)
Mà \(ƯCLN\left(a,b\right)=13\)
\(\Rightarrow\dfrac{a}{b}\) sau khi rút gọn cho 13 sẽ bằng \(\dfrac{2}{3}\)
Vậy \(\dfrac{a}{b}=\dfrac{2.13}{3.13}=\dfrac{26}{39}\)
Trước hết ta đưa \(\dfrac{18}{27}\) về phân số tối giản. Ta có:\(\dfrac{18}{27}=\dfrac{2}{3}\)
\(\dfrac{2.13}{3.13}=\dfrac{26}{39}\)
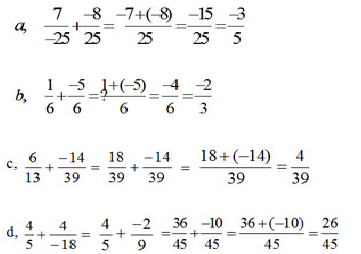


\(\dfrac{-4}{50}\text{=}\dfrac{-2}{25}\)
\(\dfrac{6}{25}\text{=}\dfrac{6}{25}\)
\(\dfrac{-27}{54}\text{=}\dfrac{-1}{2}\)
\(\dfrac{-18}{-75}\text{=}\dfrac{6}{25}\)
\(\dfrac{28}{-56}\text{=}-\dfrac{1}{2}\)
suy ra chỉ có phân số \(\dfrac{-4}{50}\) là không bằng phân số nào trong các phân số còn lại
-1/2