Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Gọi năng suất chở hàng theo kế hoạch là x ( tấn / ngày; x > 0 )
⇒ Năng suất chở hàng theo thực tế là x + 5 ( tấn / ngày )
⇒ Thời gian hoàn thành công việc theo kế hoạch là \(\dfrac{150}{x}\left(ngày\right)\)
⇒ Thời gian hoàn thành công việc theo thực tế là \(\dfrac{160}{x+5}\left(ngày\right)\)
Theo đề bài, thời gian hoàn thành công việc theo kế hoạch nhiều hơn thực tế là 1 ngày.
\(\Rightarrow\dfrac{150}{x}-\dfrac{160}{x+5}=1\)
\(\Leftrightarrow\dfrac{150\left(x+5\right)}{x\left(x+5\right)}-\dfrac{160x}{x\left(x+5\right)}-\dfrac{x\left(x+5\right)}{x\left(x+5\right)}=0\)
\(\Rightarrow150x+750-160x-x^2+5x=0\)
\(\Leftrightarrow-x^2-5x+750=0\)
\(\Leftrightarrow x^2+5x-750=0\)
\(\Leftrightarrow\left(x+30\right)\left(x-25\right)=0\)
\(\Rightarrow\left[{}\begin{matrix}x+30=0\\x-25=0\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=-30\left(loại\right)\\x=25\left(tm\right)\end{matrix}\right.\)
sai rồi bạn ơi
chỗ -x(x+5) thì thay vì là -x^2+5x thì phải là -x^2-5x chứ bạn quên đổi dấu à

Lời giải:
Giả sử theo kế hoạch đội xe chở 140 tấn hàng hết $a$ ngày, nghĩa là mỗi ngày đội chở $\frac{140}{a}$ tấn hàng.
Theo bài ra ta có:
$(\frac{140}{a}+5)(a-1)=140+10$
$\Leftrightarrow \frac{-140}{a}+5a=15$
$\Leftrightarrow \frac{-28}{a}+a=3$
$\Leftrightarrow a^2-3a-28=0$
$\Leftrightarrow (a-7)(a+4)=0$
$\Rightarrow a=7$
Tức là theo kế hoạch đội sẽ chở hàng trong 7 ngày.

Gọi thời gian để đội xe chở hết số hàng theo kế hoạch là x (x>0, ngày)
Số sản phẩm theo kế hoạch đội phải chở là \(140x\) (tấn)
Số sản phẩm đội chở được theo thực tế là \(140x+10\) (tấn)
Thời gian thực tế là đội làm là \(x-1\) (ngày)
Mỗi ngày thực tế đội chở được số tấn hàng là \(\dfrac{140x+10}{x-1}\) (tấn/ngày)
Vì thực tế mỗi ngày đội chở vượt mức 5 tấn so với dự định
\(\to\) Ta có pt: \(\dfrac{140x+10}{x-1}-140=5\)
\(\leftrightarrow \dfrac{140x+10}{x-1}=145\)
\(\leftrightarrow 140x+10=145(x-1)\)
\(\leftrightarrow 140x+10=145x-145\)
\(\leftrightarrow 140x-145x=-145-10\)
\(\leftrightarrow -5x=-155\)
\(\leftrightarrow x=31\) (TM)
Vậy thời gian đội chở số hàng theo dự định là 31 ngày

Gọi thời gian đội xe đó phải chở theo kế hoạch là a (ngày) (\(a\inℕ^∗\))
=> Thời gian đội xe đó đã chở theo thực tế là a - 1 (ngày)
Năng suất chở của đội xe theo kế hoạch là \(\frac{140}{a}\)(tấn/ngày)
Thực tế năng suất chở của đội xe đó là \(\frac{150}{a-1}\)(tấn/ngày)
Do mỗi ngày đội đó chở vượt mức 5 tấn nên ta có phương trình: \(\frac{150}{a-1}-\frac{140}{a}=5\)
\(\Leftrightarrow\)\(150a-140a+140=5a\left(a-1\right)\)
\(\Leftrightarrow\)\(10a+140=5a^2-5a\)
\(\Leftrightarrow\)\(5a^2-15a-140=0\)
\(\Leftrightarrow\)\(\left(a-7\right)\left(a+4\right)=0\)
\(\Leftrightarrow\)a = 7 hoặc a = -4 (a = -4 loại do thời gian không thể âm)
Vậy theo kế hoạch đội xe phải chở trong 7 ngày.
gọi số ngày đội chở hết hàng là x(x>1 ngày)
mỗi ngày đội trở được số hàng là 140/x( tấn hàng)
do vượt quá mức nên số ngày đội đã chở được là 140/x-1(ngày)
Theo bài ra. ta có:
(140/x-1).(x+5)=140+10
tương đương:(140-x).(x+5)=150x
tương đương:140x+700-5x-x^2+150x
tương đương: x^2+15x-700=0
Ta có: x.(x+15)=700
ta có bảng gt sau:
x 20 -20
x+15 35 -35
còn lại mấy trường hợp nữa bạn tự giải ra
ta có x=20 tmdkdb
vậy kế hoạch phải chở hàng hết 140:20=7(ngày)

Gọi số tấn hàng phải chở là x
Theo đề, ta có: x/40-(x+10)/50=1
=>1/200x=1+1/5=6/5
=>x=6/5*200=240

Gọi số sản phẩm tổ dự định làm theo kế hoạch là x (sản phẩm, ).
Thiết lập được PT:
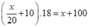
Từ đó tìm được x = 800 (sản phẩm)

Gọi số ngày dự định chở số hàng là a (a > 0)
Mỗi ngày theo dự định chở được \(\dfrac{140}{a}\) (tấn hàng)
Thực tế số hàng đội đó chở được mỗi ngày là : \(\dfrac{140}{x}+5\)( tấn hàng)
Do vậy đội đã hoàn thành sớm hơn 1 ngày và vượt mức quy định 10 tấn nên ta có hpt :
\(\dfrac{140}{x}+5\) = \(\dfrac{140+10}{x-1}\)
Giải hệ, ta được x = 7
Vậy đội đó dự nđịnh chở số hàng trong 7 ngày.
Gọi năng suất dự tính theo kế hoạch mỗi ngày vận chuyển được \(x\)(tấn hàng) \(x\inℕ^∗\).
Thời gian vận chuyển xong theo dự tính là \(\frac{180}{x}\)(ngày) .
Thực tế mỗi ngày vận chuyển được: \(x+1\)(tấn).
Thời gian là: \(\frac{180}{x}-1\)(ngày) .
Ta có phương trình:
\(\left(x+1\right)\left(\frac{180}{x}-1\right)=180+10\)
\(\Leftrightarrow180+\frac{180}{x}-x-1=190\)
\(\Leftrightarrow\orbr{\begin{cases}x=9\left(tm\right)\\x=-20\left(l\right)\end{cases}}\)
Vậy theo kế hoạch mỗi ngày vận chuyển được \(9\)tấn, xong trong \(\frac{180}{9}=20\)ngày.