Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Ta có:
\(\begin{array}{l}P + Q = \left( {2{x^2}y - x{y^2} + 22} \right) + \left( {x{y^2} - 2{x^2}y + 23} \right)\\ = 2{x^2}y - x{y^2} + 22 + x{y^2} - 2{x^2}y + 23\\ = \left( {2{x^2}y - 2{x^2}y} \right) + \left( { - x{y^2} + x{y^2}} \right) + \left( {22 + 23} \right)\\ = 45.\end{array}\)
Quan sát cột có tổng P + Q khác 45 thì cột đó có kết quả sai.
Như vậy cột 3 có kết quả sai.
- Học sinh 1: (đề số 1) 2(x -2) + 1 = x - 1
⇔ 2x – 4 – 1 = x -1 ⇔ x = 2
- Học sinh 2: (đề số 2) Thay x = 2 vào phương trình ta được:
(2 + 3)y = 2 + y ⇔ 5y = 2 + y ⇔ y = 1/2
- Học sinh 3: (đề số 3) Thay y = 1/2 vào phương trình ta được:
- Học sinh 4 (đề số 4) thay z = 2/3 vào phương trình ta được:
Vậy t = 2.
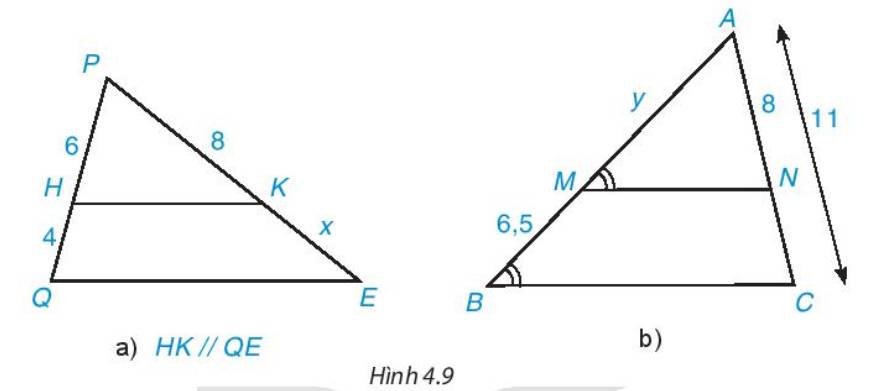
• Hình 4.9a)
Vì HK // QE nên áp dụng định lí Thalès, ta có:
\(\dfrac{{PH}}{{QH}} = \dfrac{{PK}}{{KE}}\)hay \(\dfrac{6}{4} = \dfrac{8}{x}\)
Suy ra \(x = \dfrac{{8.4}}{6} = \dfrac{{16}}{3} \approx 5,3\) (đvđd).
• Hình 4.9b)
Vì \(\widehat {AMN} = \widehat {ABC};\widehat {AMN}\) và \(\widehat {ABC}\) là hai góc đồng vị nên MN // BC.
Ta có AB = AM + BM = y + 6,5.
Áp dụng định lí Thalès, ta có: \(\dfrac{{AM}}{{AB}} = \dfrac{{AN}}{{AC}}\) hay \(\dfrac{y}{{y + 6,5}} = \dfrac{8}{{11}}\)
Suy ra 11y = 8(y + 6,5)
11y = 8y + 52
11y – 8y = 52
3y = 52
\(y = \dfrac{{52}}{3} \approx 17,3\) (đvđd)
Vậy x ≈ 5,3 (đvđd); y ≈ 17,3 (đvđd).
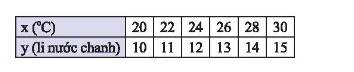
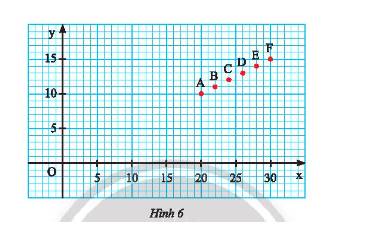
a) Điểm \(A\left( {20;10} \right);B\left( {22;11} \right);C\left( {24;12} \right);D\left( {26;13} \right);E\left( {28;14} \right);D\left( {30;15} \right)\)
Ta thấy mỗi cặp giá trị \(x;y\) tương ứng trong bảng là tọa độ của các điểm \(A;B;C;D;E;F\).
a) Phân thức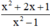 
xác định
⇔ x2 – 1 ≠ 0
⇔ (x – 1)(x + 1) ≠ 0
⇔ x – 1 ≠ 0 và x + 1 ≠ 0
⇔ x ≠ ±1
Vậy phân thức xác định với mọi x ≠ ±1
b) Với x ≠ ±1, ta có:
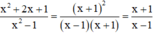
c) + Với x = 2, bạn Thắng tính giá trị biểu thức đúng.
+ Với x = -1, phân thức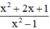 
không xác định nên không thể tính giá trị biểu thức nên bạn Thắng tính sai.
+ Để tính giá trị của phân thức bằng cách tính giá trị của phân thức rút gọn, ta phải đảm bảo giá trị của biến thỏa mãn điều kiện xác định.
a) Biểu đồ thích hợp để biểu diễn các số liệu trong bảng là: Biểu đồ cột
b)
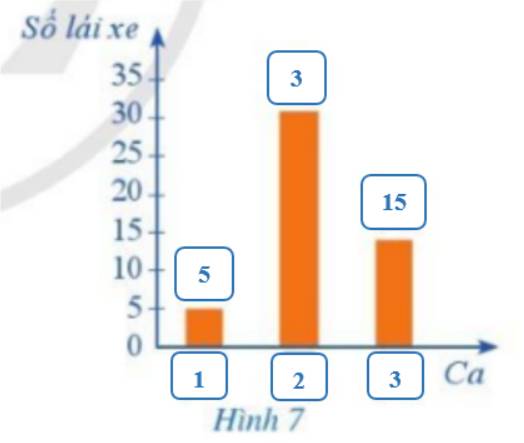
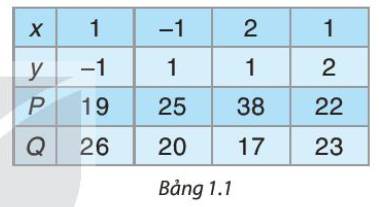
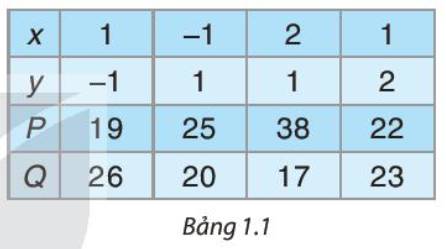
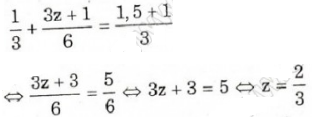
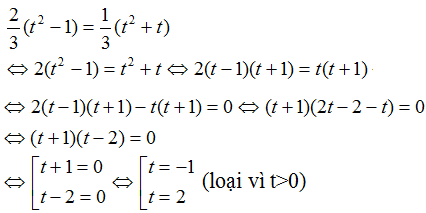
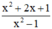
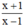
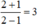
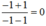
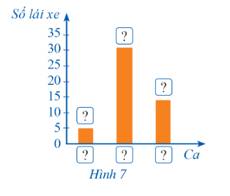
Ta có:
\(\begin{array}{l}P + Q = \left( {2{x^2}y - x{y^2} + 22} \right) + \left( {x{y^2} - 2{x^2}y + 23} \right)\\ = 2{x^2}y - x{y^2} + 22 + x{y^2} - 2{x^2}y + 23\\ = \left( {2{x^2}y - 2{x^2}y} \right) + \left( { - x{y^2} + x{y^2}} \right) + \left( {22 + 23} \right)\\ = 45.\end{array}\)
Quan sát cột có tổng P+Q khác 45 thì cột đó có kết quả sai.
Như vậy cột 3 có kết quả sai.