Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Thí nghiệm của Niuton về sự tán sắc ánh sáng:
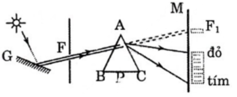
Hình 24.1
Chiếu một chùm ánh sáng trắng (ánh sáng Mặt Trời), song song qua khe hẹp F. Đặt một màn M song song với khe F. Giữa khe F và màn M, đặt một lăng kính (P), sao cho cạnh khúc xạ của (P) song song với F. Chùm tia sáng ló ra khỏi lăng kính không những bị lệch về phía đáy lăng kính, mà còn bị tách ra thành nhiều chùm sáng có màu sắc khác nhau. Trên màn M, ta thu được một dải màu biến thiên liên tục gồm 7 màu chính: đỏ, cam, vàng, lục, lam, chàm, tím. Dải sáng màu này gọi là quang phổ của Mặt Trời.

Chọn đáp án B.
Thí nghiệm với ánh sáng đơn sắc của Niuton nhằm chứng minh: Lăng kính không làm thay đổi màu sắc của ánh sáng qua nó.

Trong thí nghiệm với ánh sáng đơn sắc của Niuton, nếu ta bỏ màn M đi rồi đưa hai lăng kính lại sát nhau, nhưng vẫn đặt ngược chiều nhau thì ánh sáng không còn bị tán sắc, trên màn M’ ta thu được vệt sáng có màu trắng, nhưng viền đỏ ở cạch trên và viền tím ở cạnh dưới.
Lý do theo tính chất thuận nghịch của chiều truyền ánh sáng thì sau khi đi qua lăng kính P’, các chùm đơn sắc lại bị lệch ngược trở lại và chúng chồng chất lên nhau trên màn M’. Vì ánh sáng ban đầu chiếu vào lăng kính P là ánh sáng trắng nên không thể coi đó là thí nghiệm tổng hợp ánh sáng trắng được.

Khi có tia ló ra khỏi lăng kính thì tia ló bao giờ cũng lệch về đáy lăng kính so với tia tới.

Tóm tắt:
a = \(10^{-3}m\)
D = \(1,25m\)
\(\lambda_1=0,64\mu m\)
\(\lambda_2=0,48\mu m\)
\(\Delta x=?\)
Giải:
Khi vân sáng trùng nhau:
\(k_1\lambda_1=k_2\lambda_2\Rightarrow\)\(\frac{k_1}{k_2}=\frac{\lambda_2}{\lambda_1}=\frac{0,48}{0,64}=\frac{3}{4}\)
Vậy: \(k_1=3;k_2=4\)\(\Rightarrow\Delta x=3i_1=3.\frac{\lambda_1.D}{a}=3.\)\(\frac{0,64.10^{-6}.1,25}{10^{-3}}=2,4.10^{-3}m=2,4mm\)
\(\rightarrow D\)

Theo đề bài: Với bức xạ λ1 thì 10i1 = MN = 20mm → i1 = 2mm.
\(\frac{\iota_1}{\iota_2}=\frac{\text{λ}_1}{\text{λ}_2}=\frac{3}{5}\)\(\rightarrow\iota_2=\frac{10}{3}mm\rightarrow N_2=2.\left[\frac{MN}{2\iota_2}\right]+1=7\)

Vị trí vân sáng bậc 4 của ánh sáng đỏ: \(x_s^4 = 4. \frac{\lambda_d D}{a}\)
Tại vị trí này có vân sáng bậc \(k\) của ánh sáng có bước sóng \(\lambda\) tức là
\(x_s^4 = x_s^k<=> 4\frac{\lambda_d D}{a}= k\frac{\lambda D}{a} \)
<=> \(\lambda = \frac{4\lambda_d}{k}.\ \ (1)\)
Mà bước sóng \(\lambda\) này thỏa mãn \(0,38 \mu m \leq \lambda \leq 0,76 \mu m.\)
Thay (1) vào ta được \(0,38 \leq \frac{4\lambda_d}{k} \leq 0,76\)
<=> \( \frac{4\lambda_d }{0,76} \leq k \leq \frac{4\lambda_d}{0,38}\)
<=> \(\frac{4.0,76}{0,76} \leq k \leq \frac{4.0,76}{0,38}\)
<=> \(4 \leq k \leq 8.\)
=> \(k = 4,5,6,7,8.\)(trong đó k = 4 chính là vân sáng bậc 4 của ánh sáng đỏ)
Vậy ngoài vân sáng bậc 4 của ánh sáng đỏ ra thì còn 4 vân sáng của các ánh sáng khác tại vị trí đó.

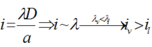
Trên màn M của thí nghiệm tán sắc ánh sáng, Niu-tơn rạch một khe hẹp F’ song song với khe F, để tách ra một chùm sáng hẹp, chỉ có màu vàng. Cho chùm sáng màu vàng qua lăng kính (P’) và hướng chùm tia ló trên màn M’, vệt sáng trên màn M’, vẫn bị lệch về phía đáy của lăng kính (P’) nhưng vẫn giữ nguyên màu vàng.
Làm thí nghiệm với các màu khác, kết quả vẫn như thế. Tức là chùm sáng có một màu nào đó tách ra từ quang phổ của Mặt Trời, sau khi qua lăng kính P’ chỉ bị lệch mà không bị đổi màu. Niu-tơn gọi chùm sáng này là chùm sáng đơn sắc.
Vậy ánh sáng đơn sắc là ánh sáng có một màu nhất định và không bị tán sắc khi qua lăng kính.