
Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.




Ta có: \(\sqrt{\dfrac{1}{x^2}+\dfrac{1}{y^2}+\dfrac{1}{z^2}}\)
\(=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2-2\cdot\left(\dfrac{1}{xy}+\dfrac{1}{yz}+\dfrac{1}{xz}\right)}\)
\(=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2-2\cdot\dfrac{x+y+z}{xyz}}\)
\(=\sqrt{\left(\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right)^2}\)
\(=\left|\dfrac{1}{x}+\dfrac{1}{y}+\dfrac{1}{z}\right|\)

Bài 1:
a: Áp dụng định lí Pytago vào ΔABC vuông tại A, ta được:
\(BC^2=AB^2+AC^2\)
\(\Leftrightarrow BC^2=6^2+8^2=100\)
hay BC=10(cm)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔABC vuông tại A có AH là đường cao ứng với cạnh huyền BC, ta được:
\(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}BH=3.6\left(cm\right)\\CH=6.4\left(cm\right)\end{matrix}\right.\)
b: Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHB vuông tại H có HF là đường cao ứng với cạnh huyền AB, ta được:
\(AF\cdot AB=AH^2\left(1\right)\)
Áp dụng hệ thức lượng trong tam giác vuông vào ΔAHC vuông tại H có HE là đường cao ứng với cạnh huyền AC, ta được:
\(AE\cdot AC=AH^2\left(2\right)\)
Từ (1) và (2) suy ra \(AF\cdot AB=AE\cdot AC\)

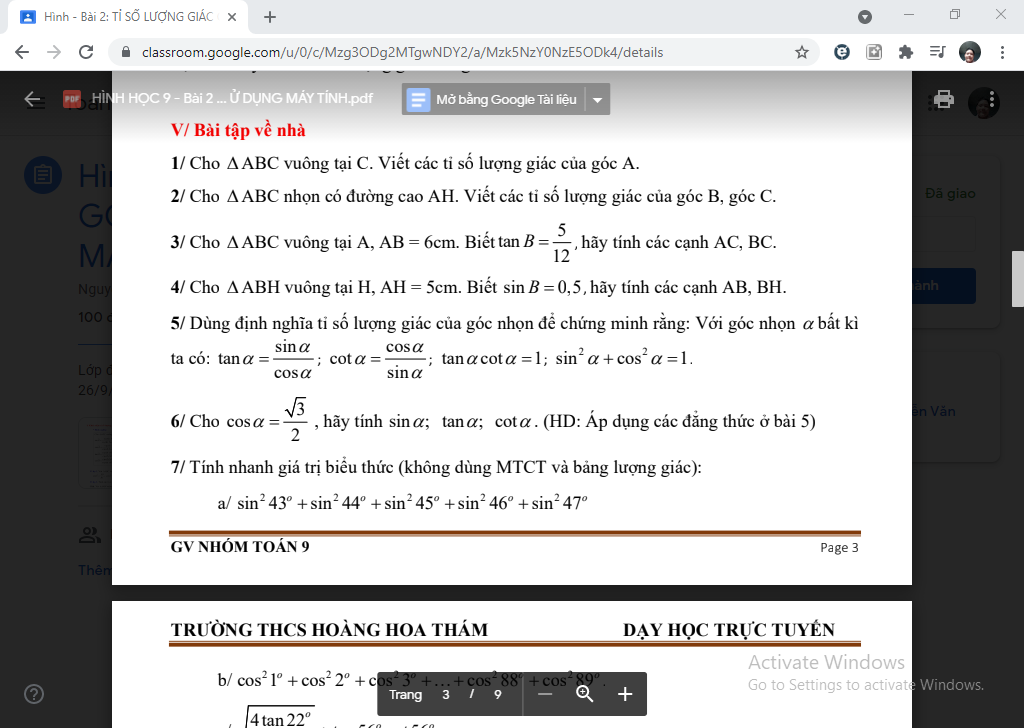
Bài 1:
\(\sin\widehat{A}=\dfrac{BC}{BA}\)
\(\cos\widehat{A}=\dfrac{CA}{AB}\)
\(\tan\widehat{A}=\dfrac{BC}{CA}\)
\(\cot\widehat{A}=\dfrac{CA}{BC}\)

b: =(m-1)^2-4(-m^2-2)
=m^2+2m+1+4m^2+8
=5m^2+2m+9
=5(m^2+2/5m+9/5)
=5(m^2+2*m*1/5+1/25+44/25)
=5(m+1/5)^2+44/5>=44/5>0 với mọi m
=>PT luôn có hai nghiệm pb

ĐKXĐ: \(x\ge1\)
\(\sqrt{x-1-4\sqrt{x-1}+4}+\sqrt{x-1-6\sqrt{x-1}+9}=0\)
\(\Leftrightarrow\sqrt{\left(\sqrt{x-1}-2\right)^2}+\sqrt{\left(3-\sqrt{x-1}\right)^2}=0\)
\(\Leftrightarrow\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|=0\)
Do \(\left|\sqrt{x-1}-2\right|+\left|3-\sqrt{x-1}\right|\ge\left|\sqrt{x-1}-2+3-\sqrt{x-1}\right|=1>0\) với mọi x thuộc TXĐ
\(\Rightarrow\) Phương trình đã cho vô nghiệm


a) Ta có: \(A=\left(\dfrac{x}{x-4}+\dfrac{1}{\sqrt{x}-2}+\dfrac{1}{\sqrt{x}+2}\right):\dfrac{\sqrt{x}}{\sqrt{x}+2}\)
\(=\dfrac{x+\sqrt{x}+2+\sqrt{x}-2}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\cdot\dfrac{\sqrt{x}+2}{\sqrt{x}}\)
\(=\dfrac{x+2\sqrt{x}}{\sqrt{x}-2}\cdot\dfrac{1}{\sqrt{x}}\)
\(=\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\)
b) Thay \(x=7+4\sqrt{3}\) vào A, ta được:
\(A=\dfrac{2+\sqrt{3}+2}{2+\sqrt{3}-2}=\dfrac{4+\sqrt{3}}{\sqrt{3}}=\dfrac{4\sqrt{3}+3}{3}\)
c) Ta có: \(M=\dfrac{x+5}{\sqrt{x}-2}:\dfrac{\sqrt{x}+2}{\sqrt{x}-2}\)
\(=\dfrac{x+5}{\sqrt{x}-2}\cdot\dfrac{\sqrt{x}-2}{\sqrt{x}+2}\)
\(=\dfrac{x+5}{\sqrt{x}+2}\)
\(=\sqrt{x}+2+\dfrac{9}{\sqrt{x}+2}-4\)
\(\Leftrightarrow M\ge2\cdot\sqrt{\left(\sqrt{x}+2\right)\cdot\dfrac{9}{\sqrt{x}+2}}-4\)
\(\Leftrightarrow M\ge2\cdot3-4=6-4=2\)
Dấu '=' xảy ra khi \(\sqrt{x}+2=3\)
\(\Leftrightarrow\sqrt{x}=1\)
hay x=1








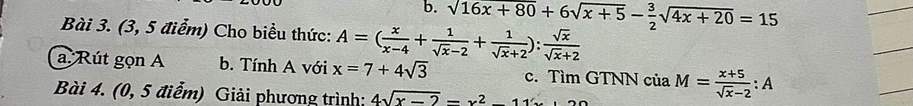 mn giúp em phần tìm gtnn vs ạ, em cần gấp
mn giúp em phần tìm gtnn vs ạ, em cần gấp
bài 5
ta có : \(M=\frac{\sqrt{x}-2+5}{\sqrt{x}-2}=1+\frac{5}{\sqrt{x}-2}\) nhỏ nhất khi \(\sqrt{x}-2\) là số âm lớn nhất có thể
\(\Rightarrow x=3\)
bài 6. ta có :
\(P=\frac{9x-1+1}{3\sqrt{x}-1}=3\sqrt{x}+1+\frac{1}{3\sqrt{x}-1}=3\sqrt{x}-1+\frac{1}{3\sqrt{x}-1}+2\ge2+2=4\)
vậy GTNN của P=4 khi \(3\sqrt{x}-1=1\Leftrightarrow x=\frac{4}{9}\)