Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Nguyên nhân chủ yếu gây nên sai số ngẫu nhiên của phép đo tiêu cự thấu kính phân kỳ trong thí nghiệm này có thể do:
- Không xác định được đúng vị trí ảnh hiện rõ nét nhất trên màn ảnh M;
- Các quang trục của thấu kính phân kì L và thấu kính hội tụ L0 chưa trùng nhau;
- Đèn Đ không đủ công suất để chiếu sáng hoặc dây tóc đèn chưa được điều chỉnh nằm ở tiêu diện của kính tụ quang (lắp ở đầu đèn Đ).
- Ngoài ra ta có: 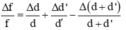
Ta thấy, khi chọn d khá lớn để Δd/d nhỏ thì d’ sẽ nhỏ. Kết quả là Δf/f sẽ lớn và gây ra sai số.

Ta sử dụng 1 sợi dây không dãn buộc một đầu vào thiết bị tạo rung khi đó tần số của sóng trên sợi dây là tần số của thiết bị tạo rung và từ đó chúng ta xác định được phương trình.

Tham khảo:
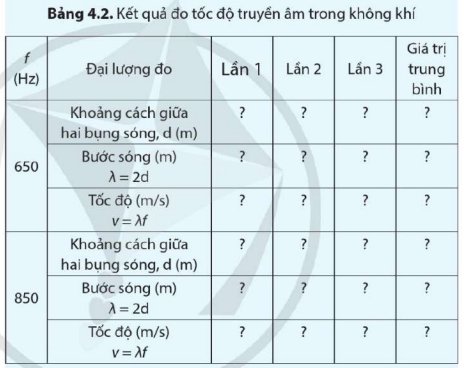
Tiến hành thí nghiệm và có bảng kết quả như bài trên, sử dụng kết quả đó để tính sai số.
Với f = 650 Hz:
\(\overline{d}=\dfrac{d_1+d_2+d_3}{3}=0,25\left(m\right)\)
\(\overline{\lambda}=\dfrac{\lambda_1+\lambda_2+\lambda_3}{3}=0,5\left(m\right)\)
\(\overline{v}=\dfrac{v_1+v_2+v_3}{3}=325\left(m/s\right)\)
Sai số của d: \(\overline{\Delta d}=\dfrac{\Delta d_1+\Delta d_2+\Delta d_3}{3}=0,007\)
Sai số của \(\lambda\): \(\overline{\Delta\lambda}=\dfrac{\Delta\lambda_1+\Delta\lambda_2+\Delta\lambda_3}{3}=0,013\)
Sai số của v: \(\overline{\Delta v}=\dfrac{\Delta v_1+\Delta v_2+\Delta v_3}{3}=8,667\)

1. Dạng đồ thị và mối quan hệ U và I đối với pin cũ và pin mới là dạng đồ thị của hàm số bậc nhất nghịch biến, mối quan hệ giữa U và I là tỉ lệ nghịch với nhau.
2. Có thể sử dụng phương án:
a. Từ \(I = {I_A} = \frac{E}{{R + {R_A} + {R_0} + r}} \Rightarrow \frac{1}{I} = \frac{1}{E}\left( {R + {R_A} + {R_0} + r} \right)\)
đặt y = \(\frac{1}{x}\); x = R; b = RA + R0 + r ⇒ y = \(\frac{1}{E}\left( {x + b} \right)\)
b. Căn cứ các giá trị của R và I trong phương án 1, ta tính các giá trị tương ứng của x và y.
c. Vẽ đồ thị y = f (x) biểu diễn gián tiếp mối liên hệ giữa I và R.
d. Xác định tọa độ của xm và y0 là các điểm mà đồ thị trên cắt trục hoành và trục tung.
\(\left\{ \begin{array}{l}y = 0 \to {x_m} = - b = - \left( {{R_A} + {R_0} + r} \right) \to r\\x = 0 \to {y_0} = \frac{b}{E} \to E\end{array} \right.\)

Tính giá trị trung bình: \(\overline A = \frac{{{A_1} + {A_2} + ... + {A_n}}}{n}\)
- Xác định sai số tuyệt đối ứng với mỗi lần đo là trị tuyệt đối của hiệu giữa giá trị trung bình và giá trị của mỗi lần đo
\(\Delta \overline {{A_1}} = \left| {\overline A - \left. {{A_1}} \right|} \right.\)
\(\Delta \overline {{A_2}} = \left| {\overline A - \left. {{A_2}} \right|} \right.\)
…
\(\Delta \overline {{A_n}} = \left| {\overline A - \left. {{A_n}} \right|} \right.\)
- Tính sai số tuyệt đối trung bình của n lần đo gọi là sai số ngẫu nhiên:
\(\overline A = \frac{{\Delta {A_1} + \Delta {A_2} + ... + \Delta {A_n}}}{n}\)
- Sai số tuyệt đối của phép đo là tổng sai số ngẫu nhiên và sai số dụng cụ:
\(\Delta A = \Delta \overline A + \Delta A'\)