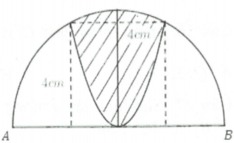
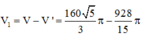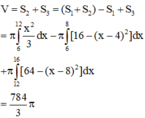Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
a) Vì tia Ot là tia phân giác của \(\widehat{xOy}\)
=> \(\widehat{xOt}=\widehat{yOt}=\dfrac{\widehat{xOy}}{2}=\dfrac{70^o}{2}=35^o\)
Vậy \(\widehat{yOt}=35^o\)
b) Trên cùng 1 nửa mặt phẳng bờ chứa tia Ox có :
\(\widehat{xOy}=70^o< \widehat{xOz}=90^o\)
=> Tia Oy nằm giữa tia Ox và tia Oz
=> \(\widehat{xOy}+\widehat{yOz}=\widehat{xOz}\left(1\right)\)
Thay \(\widehat{xOy}=70^o\) và \(\widehat{xOz}=90^o\) vào (1) , ta được :
\(70^o+\widehat{yOz}=90^o\)
=> \(\widehat{yOz}=90^o-70^o=20^o\)
Vậy \(\widehat{yOz}=20^o\)
Cặp góc phụ nhau có trong hình là \(\widehat{xOy}\) và \(\widehat{yOz}\)
Đáp án A
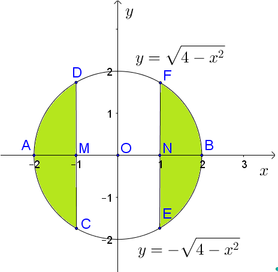
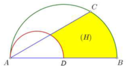
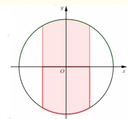Chọn hệ trục tọa độ Oxy như hình vẽ với O là gốc tọa độ. Phương trình đường tròn tâm O, đường kính AB = 8 là
x
2
+
y
2
=
16
⇔
y
2
=
16
-
x
2
⇔
x
=
±
16
-
x
2
.
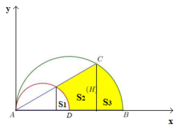
Diện tích hình phẳng cần tính gấp 2 lần diện tích hình phẳng (H) giới hạn bởi đồ thị hàm số y = 16 - x 2 , y = 0 , x = - 2 , x = 2 .
Khi đó S = 2 . S H = 2 . ∫ - 2 2 16 - x 2 d x ⇒ S = S = 16 3 π + 8 3 .
Đáp án B.
Phương pháp: Ứng dụng tích phân để tính thể tích khối tròn xoay.
Cách giải: Gắn hệ trục tọa độ Oxy như hình vẽ:
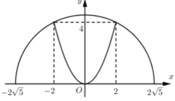
Ta có:
Phương trình đường tròn: 
Phương trình parabol: 
Thể tích khối cầu 
Thể tích khi quay phần tô đậm quanh trục Ox là: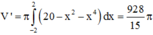 
=> Thể tích cần tính 
