Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.
Bài 2:
a: Vì AM<ÂN
nên điểm M nằm giữa hai điểm A và N
b: MN=AN-AM=5cm
c: PM=PA+AM=3+2=5cm
d: VìMP=MN
và P,M,N thẳng hàng
nên M là trung điểm của PN
a: AB=5-3=2cm
b: Trên tia BC, ta có: BC<BD
nên điểm C nằm giữa hai điểm B và D
=>BC+CD=BD
=>CD=2cm
=>AB=CD
Xét ΔABC và ΔADE có
AB=AD
\(\widehat{BAC}\) chung
AC=AE
Do đó: ΔABC=ΔADE
Suy ra: \(\widehat{MCD}=\widehat{MEB}\)
Xét ΔCBE và ΔEDC có
CB=ED
CE chung
BE=DC
Do đó: ΔCBE=ΔEDC
Suy ra: \(\widehat{MBE}=\widehat{MDC}\)
Xét ΔMBE và ΔMDC có
\(\widehat{MBE}=\widehat{MDC}\)
BE=DC
\(\widehat{MEB}=\widehat{MCD}\)
Do đó: ΔMBE=ΔMDC
Suy ra: ME=MC
Xét ΔAME và ΔAMC có
AM chung
ME=MC
AE=AC
Do đó: ΔAME=ΔAMC
Suy ra: \(\widehat{EAM}=\widehat{CAM}\)
hay AM là tia phân giác của góc xAy
– Trên đoạn MA, lấy điểm C sao cho MC = MB
Nhận thấy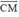 
và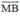 
cùng hướng nên 
= 
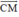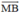
Khi đó:
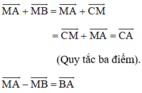
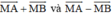
a; AM<AB
nên điểm M nằm giữa A và B
=>MB=AB-AM=4cm
b: M nằm giữa A và B
mà MA=MB
nen M là trung điểm của AB