Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

x N B A C M x'
Vì B thuộc tia Ax
C thuộc tia Ax'(đối Ax)
=> A nằm giữa B và C
=> AB + AC = BC
=> BC = 14 cm
Có : AC = 7cm, AB = 7 cm ; BC = 14cm
=> AC = AB = BC/2
=> A là trung điểm BC
b) Có AC < AM (7cm < 9 cm)
=> C nằm giữa A và M
=> AC + CM = AM
=> CM = 2cm
Vì B thuộc tia Ax
M thuộc tia Ax'
=> A nằm giữa B và M
=> AB + AM = BM
=> BM = 16 cm

Vì AD<AB(vì 1cm<2cm)nên điểm A nằm giữa 2 điểm D và B.
Ta có: AD+AB=DB
1 +2=DB
3 =DB
B không phải là trung điểm của đoạn thẳng DC vì B nằm giữa C và D nhưng B không cách đều C và D
Tick cho mình nhé bạn Võ Ngọc Thùy

a) BC=4cm
b) MB=MC=BC/2=2cm
c) phải. vì AD=2 . AB=2 . AD là tia đối của Ax
=) A là trung điểm của BD.
d) MD=DB+BM=6cm
a, Trên tia Ax, có AB<AC(vì 2cm<6cm)
=>B nằm giữa A và C
Ta có: AB+BC=AC
Mà AB=2cm;AC=6cm
=>2+BC=6
=>BC=6-2
=>BC=4(cm)
Vậy BC=4cm
b, Vì M là trung điểm của BC nên
=> M nằm giữa B và C; MB=MC
Ta có: BM+MC=BC
Mà BM=MC; BC=4cm
=> BM+BM=4
=> 2BM=4
=> BM=4:2
=> BM=2(cm)
Vậy BM=2cm
c, Vì D thuộc tia đối của tia AB nên A nằm giữa D và B (1)
Vì AB=2cm
AD=2cm
=>AB=AD(2cm) (2)
Từ (1) và (2) => A là trung điểm của DB (đpcm)

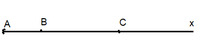
a. ta có :
\(AB+BC=AC\\ hay2+BC=7\\ \Rightarrow BC=7-2=5\left(cm\right)\)
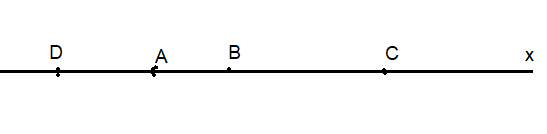
b. ta có :
\(BD-AB=AD\\ hayBD-2=3\\ \Rightarrow BD=3+2=5\left(cm\right)\)
c. ta có :
\(DC-BD=BC\\ hayDC-5=5\\ \Rightarrow DC=5+5=10\left(cm\right)\)
ta thấy \(BD=BC=\dfrac{DC}{2}=\dfrac{10}{2}=5\left(cm\right)\)
nên B là trung điểm DC

a, Trên tia Ay, có 2 điểm B và C sao cho AB = 2 cm , AC = 5 cm ( AB < AC )
=> điểm B nằm giữa 2 điểm A và C
Suy ra : AB + BC = AC
2 + BC = 5
BC = 5 - 2 = 3 ( cm)
b, Vì điểm D trên tia Ax , điểm C trên tia Ay
Nên điểm A nằm giữa 2 điểm D và C
Mà AD = AC
Suy ra điểm a là trung điểm của DC

a, Ta có:
AB = AC + BC
\(\Rightarrow\)BC = AB - AC = 7 -3 = 4 (cm)
b,
Vì D là trung điểm của AC nên DC = 1/2 AC = 1.5 (cm)
Đoạn BD = BC + DC = 4 +1.5 = 4.5 (cm)
c, Đoạn AE = AC + CE = 3 + 1 = 4( cm)
Đoạn AB = 7(cm) > 4 (cm)
\(\Rightarrow\)Điểm B nằm ngoài đoạn AE . Vậy điểm B không phải truang điểm của đoạn AE