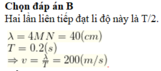Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Đáp án D
Khoảng cách giữa bụng và nút gần nhất là MN = 0,25λ → λ = 40 cm.
Khoảng thời gian để trung điểm MN có cùng li độ với điểm M là nửa chu kì → T = 0,2 s.
+ Tốc độ truyền sóng v = λ/T = 200 cm/s.

\(\omega=\frac{2\pi}{T}=2\pi\)(rad/s)
Vận tốc cực đại \(v_{max}=\omega A=2\pi.5=10\pi\)(cm/s)
Vì vận tốc là đại lượng biến thiên điều hòa theo thời gian, nên ta khảo sát nó bằng véc tơ quay.
10π v 5π M N -10π O
Tại thời điểm t, trạng thái của vận tốc ứng với véc tơ OM, sau 1/6 s = 1/6 T, véc tơ quay: 1/6.360 = 600
Khi đó, trạng thái của vận tốc ứng với véc tơ ON --> Vận tốc đạt giá trị cực đại là: \(10\pi\) (cm/s)
Đáp án B.

chọn Đáp án A
A là bụng với biên độ sóng là Ao C là nút gần A nhất B là trung điểm của AC
Biên độ sóng của một điểm cách C một đoạn x
A
=
A
0
sin
(
2
π
x
λ
)
Ta có
A
B
=
B
C
=
λ
8
⇒
A
B
=
A
0
2
→khoảng thời gian hai lần liên tiếp điểm A có li độ bằng biên độ của điểm B tức là tại li độ
x
A
=
A
0
2
l
à
T
4
→T=0,8 s
λ
=
4
A
C
=
40
c
m
⇒
v
=
λ
T
=
50
c
m
/
s
=
0
,
5
m
/
s

Ta có $\lambda =24cm $
Bạn vẽ hình ra .
Đoạn AB =24cm sau đó vẽ 2 bụng sóng.
Lấy M N nằm giữa sao cho MN= AB/3 = 8 cm.
Khoảng cách MN lớn nhất khi chúng nằm trên bụng và nhỏ nhất khi duỗi thẳng.
Ta có $\dfrac{MN_{lớn}}{MN_{nhỏ}} =1.25 \rightarrow MN_{lớn}=10 \rightarrow $biên độ của M và N là 3cm.
Khoảng cách từ M đến nút bằng 4cm =$\dfrac{\lambda}{6} \rightarrow A_{bụng} =2\sqrt{3}$

Hai điểm có cùng biên độ 2 mm đối xứng nhau qua nút gần nhất và hai điểm có biên độ 3 mm nằm đồi xứng nhau qua bụng gần nhất. Áp dụng công thức tình biên độ điểm, ta có hệ phương trình:
Gọi biên độ sóng tại bụng là 2a.
Ta có : \(\frac{1}{a^2}=\frac{9}{4a^2}=1\rightarrow a=\frac{2}{\sqrt{13}}\)
Xét: \(2a\sin\frac{2\pi x}{\lambda}=2\rightarrow2\lambda=54cm\Rightarrow\lambda=27cm\)
Vậy chọn đáp án A.