Hãy nhập câu hỏi của bạn vào đây, nếu là tài khoản VIP, bạn sẽ được ưu tiên trả lời.

Với quy luật: f1 = n1f0, f2 = n2f0, …, fn = nnf0 → sóng dừng trên dây có 2 đầu cố định. → Số nút bằng số bụng cộng 1.

Với quy luật: f1 = n1f0, f2 = n2f0, …, fn = nnf0® sóng dừng trên dây có 2 đầu cố định.
® Số nút bằng số bụng cộng 1.
Chọn đáp B

Sóng dừng trên dây có 2 đầu cố định thì tần số cơ bản \(f_0\) (tần số nhỏ nhất để có sóng dừng ứng với 1 bó sóng)
Thì các tần số để có sóng dừng là: \(f_n=n.f_0\)
Suy ra: \(f_0=8Hz\)
Có: \(\dfrac{1}{\lambda_{n+1}}-\dfrac{1}{\lambda_{n}}=\dfrac{f_{n+1}}{v}-\dfrac{f_{n}}{v}=\dfrac{8}{v}=0,2\Rightarrow v=40m/s\)
Tần số âm cơ bản ứng với 1 bó sóng ta có: \(l=\dfrac{\lambda}{2}=\dfrac{v}{2f_0}=\dfrac{40}{2.8}=2,5m\)
Chọn D.

Đây em nhé Câu hỏi của Nguyễn Thị Trúc Đào - Vật lý lớp 12 | Học trực tuyến
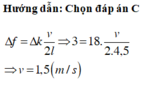
+ Với quy luật: f1 = n1f0, f2 = n2f0, …, fn = nnf0 → sóng dừng trên dây có 2 đầu cố định.
→ Số nút bằng số bụng cộng 1.
Đáp án B